Monetary authorities across the world have always devoted substantial resources to forecasting inflation. The history of monetary policy, however, suggests that the enterprise of predicting changes in the price level has had mixed success over time. In some periods, inflation appears predictable, in that multivariate models produce forecasts that are more accurate than the forecasts based on very simple “naïve” models; in other periods, however, virtually no model seems to improve upon such “naïve” models (as shown by, among others, Stock and Watson 2007 and 2008, Rossi and Sekhposyan 2010, and D’Agostino et al. 2006).
The 20th-century monetary history of the United States reveals that the monetary regimes characterised by either a clear nominal anchor or a credible anti-inflationary policy stance have been associated with lower levels of inflation (Bordo and Schwartz 1999). In a recent paper (D’Agostino and Surico 2011), we investigate whether in these regimes inflation has become harder to forecast using either money growth, as suggested by the quantity theory, or output growth, as suggested by a Phillips curve relationship.
A flexible tool to study the evolution of predictability
An historical evaluation of inflation forecasts across the regimes that characterised the US monetary history since 1900 requires a flexible statistical model to identify endogenously the dates of any possible changes in predictability, and therefore to assess whether these dates correspond to major changes in the conduct of monetary policy. A flexible forecasting tool is a Vector AutoRegression (VAR) in which both the coefficients and the volatilities are allowed, but not required, to change over time. The reason for using a time-varying statistical model is twofold.
- First, the dynamics and volatilities of inflation, money and output growth have exhibited substantial instabilities over the 20th century (Sargent and Surico 2011).
- Second, the long sample cuts across two world wars, the Great Depression, the great inflation and several monetary regimes, which differed markedly in their success to establish a credible framework to gain control over inflation.1
The estimates of the time-varying VAR and the time-varying AR models are then used to construct iteratively the sequences of forecasts for more than a hundred years from 1900 to 2007. From the forecasts we build the sequence of forecast errors implied by the three models:
- a time-varying VAR in inflation and money growth,
- a time-varying VAR in inflation and output growth, and
- a time-varying univariate autoregressive process for inflation.
The marginal predictive power of money and output growth is evaluated in the following way. First, we compute the squared forecast errors for the three models. Then, we compute a rolling average of the errors over eight years. Finally, we take the ratio between the rolling mean of squared errors obtained with the time-varying VARs and the rolling mean of squared errors obtained with the time-varying univariate autoregressive process for inflation. Values of the relative mean squared forecast errors below 1 mean that the variable included in the VAR marginally improves upon the accuracy of the univariate model for inflation.
Dating the US monetary regimes
The analysis intends to assess the evidence on the evolution of inflation predictability from the statistical models against the evidence on the evolution of monetary policy from the narrative account of the US economic history. Following Meltzer (1986), US monetary history in the 20th century is divided in six major regimes:
- From the beginning of the sample to 1931Q3: Gold standard. Ended when Britain left the gold standard.
- From 1931Q4 to 1939Q3: Mixed system. Ended with the outbreak of the Second World War.2
- From 1939Q4 to 1951Q1: pegged interest rate for most of the period. Ended with the Treasury-Federal Reserve Accord which removed the obligation to support the US government bonds market and thus allowed the Fed to pursue an independent monetary policy.
- From 1951Q2 to 1971Q3: Bretton Woods. Ended when Nixon closed the gold window.
- From 1971Q4 to 1983Q4: Great Inflation. Ended with Volcker’s disinflation.
- From 1984Q1 to the end of the sample: Great Moderation.
A similar categorisation has been used by Bordo and Haubrich (2008) to investigate the evolution of the marginal predictive power of the yield spread for output growth.
Monetary regimes and inflation predictability: The link
The two time-varying VARs relating inflation to money growth output growth are fit on US quarterly data. The benchmark model is a time-varying univariate autoregressive process for inflation.
The statistical significance of any possible improvement (or deterioration) in predictability is assessed by means of median values and the central 68% error bands of the posterior distribution of the relative mean squared forecast errors. If the value of one falls outside the error bands, then the two models generate forecasts that are statistically different from one another.
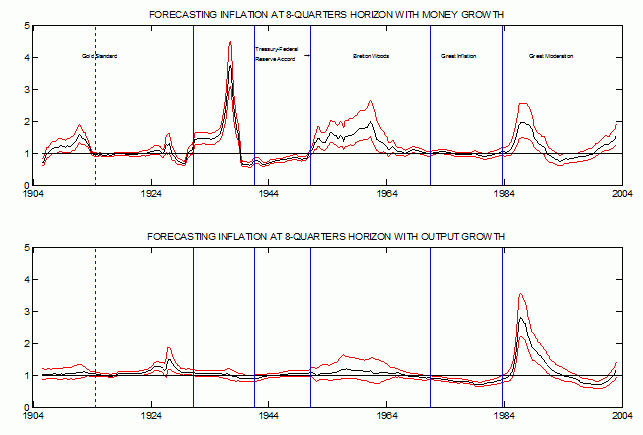
Results are reported in Figure 1. For the sake of exposition, it focuses on eight-quarters ahead forecasts, which represent the typical horizon at which central banks are expected to meet their (implicit) target. Similar results are obtained for horizons of one, four and twelve quarters. Vertical lines represent the monetary regime shifts discussed above.
Figure 1. Forecasting inflation 8-quarters ahead
Notes: in the top (bottom) panel, ratio of the rolling mean squared errors at eight-quarters horizon (h=8) between a bivariate VAR in inflation and money growth (inflation and output growth), and a univariate model for inflation. Black lines are median estimates; red lines are 68% error bands. Vertical lines represent changes in the monetary regime. Predicted variable: inflation
Four main results emerge.
- First, over the entire 20th century, inflation predictability (as measured by the relative mean squared forecast errors statistics) appears the exception rather than the rule.
- Second, the forecasts produced by the bivariate model in inflation and money growth are significantly more accurate than the forecasts produced by the univariate model only during the years between the outbreak of WWII in 1939 and the Treasury-Federal Reserve accord in 1951.
- Third, since the Federal funds rate have traded consistently above the discount rate in 1966, output growth had marginal predictive power for inflation in only two periods: (i) the years that extend from the great inflation of the 1970s to the early 1980s when Volcker built the credibility for an anti-inflationary policy stance (see Goodfriend and King 2005), and (ii) the years between 1997 and 2000 when the Fed leaned against the wind of the IT boom.
- Fourth, under the gold standard, the Bretton Woods system and most of the great moderation sample money growth and output growth had no marginal predictive power for inflation.
In summary, the results reported in this column are consistent with the idea that a policy regime which successfully stabilises inflation makes it harder to improve upon the forecasts based on “naive” models.
The views expressed in this article do not necessarily reflect those of the European Central Bank and the Eurosystem.
References
Bordo, MD and JG Haubrich (2008), “The Yield Curve as a Predictor of Growth: Long-Run Evidence, 1875-1997”, The Review of Economics and Statistics, 90:182-185.
Bordo, MD, and AJ Schwartz (1999), “Monetary Policy Regimes and Economic Performance: the historical record”, in JB Taylor and M Woodford (eds.), Handbook of Macroeconomics, 149-234.
D’Agostino, A, L Gambetti and D Giannone (2011), “Macroeconomic Forecasting and Structural Change”, Journal of Applied Econometrics, forthcoming.
D'Agostino, A, D Giannone and P Surico (2006), “(Un)Predictability and Macroeconomic Stability”, ECB Working Paper 605.
D'Agostino, A and P Surico (2011), “A Century of Inflation Forecasts”, CEPR Discussion Papers 8292. Review of Economics and Statistics, forthcoming.
Friedman, M and AJ Schwartz (1963), A Monetary History of the United States 1867-1960, Princeton University Press.
Goodfriend, M and RG King (2005), “The Incredible Volcker Disinflation”, Journal of Monetary Economics, 52:981-1015.
Meltzer, A (1986), “Some Evidence on the Comparative Uncertainty Experienced Under Different Monetary Regimes”, in CD Campbell and WR Dougan (eds.), Alternative Monetary Regimes, The Johns Hopkins University Press.
Rossi B and T Sekhposyan (2010), “Have Models’ Forecasting Performance Changed Over Time, and When?”, International Journal of Forecasting, 26(4).
Sargent, TJ and P Surico (2011), “Two Illustrations of the Quantity Theory of Money: Breakdowns and Revivals”, American Economic Review, 101(1):109-128.
Stock, J and M Watson, 2008, Phillips Curve Inflation Forecasts, Harvard University and Princeton University, unpublished manuscript.
Stock, J and M Watson (2007), “Why Has Inflation Become Harder to Forecast?”, Journal of Money, Credit and Banking, 39:3-34.
1 For the implementation and the performance of the time varying VAR in forecasting see D’Agostino et al. (2011).
2 The fourth quarter of 1941 is another plausible closing date for this period as it corresponds to the declaration of war to Germany and Japan. We prefer to draw a vertical line earlier, however, because during the period of US neutrality large-scale orders for war materials, paid by large inflow of gold stock, resulted in a sharp rise in money growth. This, together with a greatly expanded defence programme, led to a sustained increase in wholesale prices as the Fed undertook no extensive operations to offset the rapid rise in gold stock, money stock or prices (see Friedman and Schwartz, 1963, 550-553).