For more than three decades, macroeconomic models have been harshly criticised for their inability to forecast exchange rates better than the random walk model. A large number of studies have evaluated the performance of various approaches, but widespread scepticism still prevails over whether any single model outperforms the random walk in a robust way (Rossi 2013). While recent papers have shown that the mean reverting properties of the real exchange rate help to beat the random walk in forecasting the nominal exchange rate (Ca' Zorzi et al. 2016; Cheung et al. 2017), this is not what economists really desire, which is a fully-fledged general equilibrium macro model that has predictive power. Are DSGE models what we are looking for? Although frequently used in inflation and output forecasting races (Del Negro and Schorfheide 2013), they have seldom been included by the exchange rate forecasting literature. To bridge this gap, we evaluate the exchange rate forecasting performance of the state-of-the-art DSGE model of Justiniano and Preston (2010b), which is a generalisation of Galí and Monacelli’ (2005). The model features a rich cocktail of shocks that affect domestic firms’ productivity, importers’ mark-ups, households’ preferences, risk in international financial markets, and monetary policy, as well as the dynamics of three foreign variables: output, inflation, and the interest rate. Ex ante, it is not clear whether this refined technology is a help or a hindrance in forecasting terms.
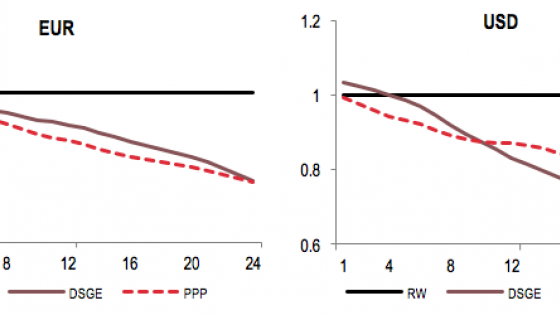
The model helps forecast the real exchange rate
At the start of this forecasting horse race we have three plausible models:
- The first model is the most widely used benchmark in the exchange rate forecasting literature, namely, the naïve random walk.
- The second model assumes that the equilibrium value of the real exchange rate is given by the relative purchasing power parity (PPP) theory. In practice, this value is calculated as the historical mean of the real exchange rate. As PPP is a long-term concept, the model also assumes that the real exchange rate convergences to its equilibrium value mean gradually (Ca’ Zorzi et al. 2016). We set the convergence pace at 5% quarterly, which implies that the half-life deviation from the PPP is slightly over three years, i.e. within the range of between three and five years proposed by Rogoff (1996) in his influential survey on the persistence of real exchange rates.
- The third competitor is the DSGE model, which we bring to the data with advanced Bayesian estimation techniques. We shall consider the real effective exchange rates of the euro and the US dollar for the period between 1975Q1 and 2013Q4.
All details about the construction of the dataset and the estimation process are available in the full version of this study (Ca’ Zorzi et al. 2017). In terms of the design of the forecasting race, we consider the recursive forecasts for horizons ranging from one quarter to six years ahead for the period 1995Q1 to 2013Q4. The out-of-sample performance is evaluated by looking at the ratios between the root mean squared forecast errors of the PPP or DSGE models and that of the random walk at different forecast horizons (Figure 1). Values below unity thus indicate that a given model forecasts better the real exchange rate than the random walk.
Figure 1 Root mean squared forecast errors for the real exchange rate relative to the random walk
Notes: The forecast horizon, shown in the horizontal axis, is expressed in quarters.
The outcome is clear. For the real exchange rate of the euro and US dollar, both the PPP and DSGE models overwhelmingly outperform the random walk, especially at longer horizons. The analysis clearly highlights that the DSGE model is useful in forecasting the real exchange rate, but that its performance is not necessarily better than that of a much simpler PPP framework. This suggests that the good performance of the model is probably not due to its rich short-term dynamics, but mainly to the built-in mean reversion mechanism of the real exchange rate.
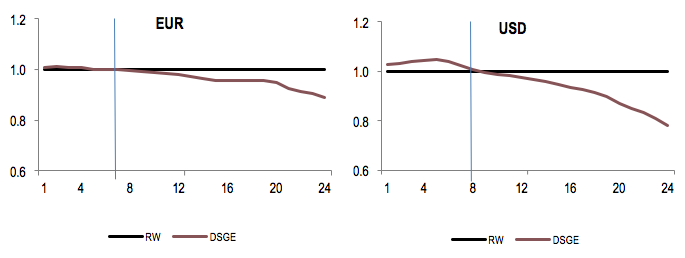
The DSGE model fails to forecast the nominal exchange rate
The ‘holy grail’ of many exchange rate economists is to find a fully-fledged economic model that helps forecast nominal and not just real exchange rate fluctuations (Rossi 2013). Our chosen DSGE model simultaneously delivers a forecast for the nominal exchange rate and the relative price index, the latter being defined here as the ratio of domestic and foreign consumer price indices. The PPP model drops from the race since it cannot deliver separate predictions for the two subcomponents of the real exchange rate. Figure 2 shows that the DSGE model performed marginally worse than the random walk for approximately the first eight quarters, and eventually better at longer horizons, as the forces of mean reversion get stronger. For all our modern technology, the 'exchange rate disconnect' puzzle – the inability of macro models to outforecast the random walk at short- to medium-term horizons – is still present.
Figure 2 Root mean squared forecast errors for the nominal exchange rate relative to the random walk
Notes: The forecast horizon, shown in the horizontal axis, is expressed in quarters.
A way to defend the DSGE set-up would be to claim that the nominal exchange rate cannot be forecast, even if the DSGE model were the true data-generating process. This hypothesis can be justified because of the forward-looking nature of exchange rates, as derived analytically by Engel and West (2005) for selected present-value models with non-stationary fundamentals, like monetary or Taylor rule models. In the full version of this study, we design a Monte Carlo experiment to show that this is not the case: with artificial data generated by the DSGE model, the nominal exchange rate should be easily forecastable (Ca’ Zorzi et al., 2017). One cannot escape the conclusion that the model is mis-specified along some important dimension.
What explains the model’s failings?
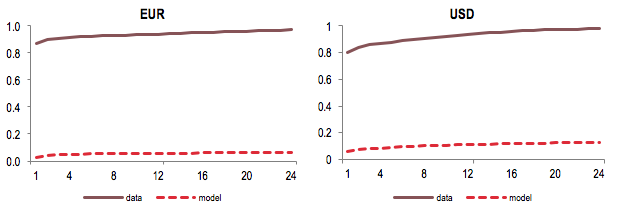
The reason the model fails to forecast the nominal exchange rate has little to do with the way the exchange rate is modelled. Somewhat ironically, the problem stems instead from the inaccuracy of its predictions for prices at home and abroad, and in particular their co-movement. Predictions of the relative price index are characterised by much higher volatility than that observed in the data. Moreover, it turns out that a simple random walk outperforms the DSGE model in forecasting the relative price index. This is revealing since the random walk can be interpreted as assuming perfect synchronisation between the dynamics of prices at home and abroad over the forecast horizon. This benchmark is less far-fetched empirically than one might think if we accept the proposition that inflation is largely a global phenomenon (Ciccarelli and Mojon 2010). Additional evidence that our forensic analysis is on the right track is found by comparing a set of moments for the data and the corresponding statistics based on the estimated DSGE model. In particular, the model implies almost no correlation between changes in domestic and foreign price indices, a far cry from what is in the data (Figure 3). This result was highlighted, in a different context, by Justiniano and Preston (2010a) as one of the key weaknesses of small open economy DSGE models.
Figure 3 Correlation of changes in domestic and foreign (log) prices at various horizons
Notes: The horizon, shown in the horizontal axis, is expressed in quarters.
We conclude that the insufficient degree of international price co-movement is the root cause of the low quality of the nominal exchange rate forecasts from the DSGE model. In particular, the excessive volatility in the relative price index requires an offsetting nominal exchange rate response to stabilise the real exchange rate, which is detrimental in forecasting terms.
Why the exchange rate is not moving randomly
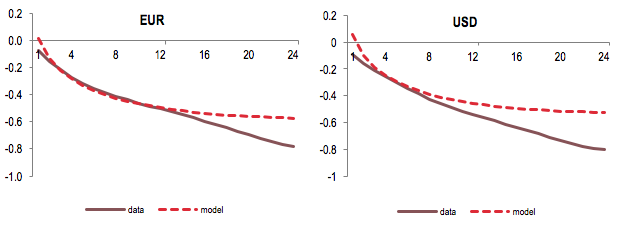
The model’s failure to beat the random walk may lead us to infer that the nominal exchange rate moves randomly. This would be learning the wrong lesson, however. In a flexible exchange rate regime, a real exchange rate adjustment can occur via changes in the nominal exchange rate or the relative price index. According to the model, for most shocks the relative price index goes in the opposite direction required to bring the real exchange rate back to its long-run equilibrium. Therefore, the real exchange rate adjustment is done almost entirely via changes in the nominal exchange rate. Crucially, this prediction of the model is consistent with the data. As shown in Figure 4, both in the model and in the data, there is a strongly negative correlation between the current real exchange rate level and the future change in the nominal exchange rate for both the US and the Eurozone. In other words, the DSGE model correctly anticipates that the nominal exchange rate plays a key role in correcting most deviations of the real exchange rate from its mean (see also Engel 2012 and Eichenbaum et al. 2017). Considering the nominal exchange rate as a random walk would miss its buffering role in flexible regimes, as already highlighted by Friedman (1953) in his classical contribution.
Figure 4 Correlation of future changes in the nominal exchange rate and the current real exchange rate level at different horizons
Notes: The horizon, shown in the horizontal axis, is expressed in quarters.
Ways to beat the random walk
We have just seen that the DSGE model fails to forecast the nominal exchange rate well, although it captures the central role of the nominal exchange rate in the adjustment of the real exchange rate. There is a simple, though draconian, way to bypass the main weakness of the model – i.e. insufficient international price co-movement – and build on its strengths, i.e. the notion that the mean reversion of the real exchange rate occurs mainly via changes in the nominal exchange rate. This can be achieved simply by imposing that changes in domestic and foreign prices over the forecast horizon are the same. This is equivalent to assuming that all the real exchange rate adjustments are achieved by changes in the nominal exchange rate. This leads to a new set of nominal exchange rate predictions that we shall call ‘partially consistent’, since they ignore the price predictions of the model. The same partial approach can be similar applied to the PPP model to get an additional set of nominal exchange rate predictions. We evaluate the performance of these two partially consistent models by including their (relative) root mean squared forecast errors in Figure 5.
Figure 5 Root mean squared forecast errors for the nominal exchange rate relative to the random walk
Note: The forecast horizon, shown in the horizontal axis, is expressed in quarters.
This reveals that both models start outperforming the random walk already at short horizons. The lesson that we draw is that, as long as mean reversion is a feature of the real exchange rate, it can be exploited to forecast the nominal exchange rate. From this, we also infer that the ability of DSGE models to forecast the nominal exchange rate would likely be strongly boosted if one could redesign them to better reflect the international synchronisation of prices. The contemporaneous success of the PPP model shows, however, that approximately the same forecasting power can be achieved without having to rely on a DSGE model.
Five lessons to remember
There is a dark cloud hanging over exchange rate economics, owing to the inability of macro models to forecast exchange rates better than just assuming that they will remain constant in the future. Every cloud has a silver lining, however. The exchange rate disconnect puzzle has spurred economists to look for new directions of research, with some success. In this column, we have reviewed the forecasting performance of a state-of-the-art open economy DSGE model. There are at least five lessons from our analysis:
- First, DSGE models are useful in forecasting the real exchange rate, even if their forecasting power is mainly due to their in-built mean reversion in the real exchange rate. The same goal can be achieved with a simple long-run PPP model.
- Second, it is misleading to think of the exchange rate as a random walk. On the contrary, there is strong evidence that it contributes significantly to restoring price competitiveness conditions in flexible exchange regimes. From this perspective, macro models provide a more accurate description of the data than the random walk.
- Third, this feature of the data can be exploited to forecast the nominal exchange rate better than with a random walk.
- Fourth, open-economy DSGE models that fail to capture international price co-movements cannot forecast the nominal exchange rate. This is clearly an area for future research. Developing macro models that exploit the mean reversion of the real exchange rate, while taking into account the international price co-movements, seems a promising way forward to improve the reliability of their exchange rate (and possibly inflation) forecasts.
- Fifth, we are far from having models that reliably connect the exchange rate to fundamentals. However, treating the nominal exchange rate as a random walk is entirely misleading, as it ignores its fundamental role as shock absorber in flexible exchange rate regimes.
Authors’ note: The views expressed are those of the authors and do not necessarily reflect those of the ECB or the Narodowy Bank Polski.
References
Ca’ Zorzi, M, J Muck and M Rubaszek (2016), “Real exchange rate forecasting and PPP: This time the random walk loses”, Open Economies Review 27(3): 585-609. See also the Vox column from 2015 at http://voxeu.org/article/time-random-walk-loses.
Ca’ Zorzi, M, M Kolasa and M Rubaszek (2017), “Exchange rate forecasting with DSGE models”, Journal of International Economics 107: 127–146.
Cheung, Y-W, M D Chinn, A G Pascual and Y Zhang (2017), “Exchange rate prediction redux: new models, new data, new currencies”, ECB Working Paper, No. 2018.
Ciccarelli, M and B Mojon (2010), “Global inflation”, The Review of Economics and Statistics 92(3): 524-535.
Del Negro, M and F Schorfheide (2013), “DSGE model-based forecasting”, in G Elliott and A Timmermann (eds), Handbook of Economic Forecasting, Volume 2, Elsevier.
Eichenbaum, M, B K Johannsen and S Rebelo (2017), “Monetary policy and the predictability of nominal exchange rates”, NBER Working Paper No. 23158.
Engel, C (2012), “Real exchange rate: The roles of price stickiness and monetary policy”, unpublished manuscript.
Friedman, M (1953), “The case for flexible exchange rates”, in M Friedman, Essays in Positive Economics, Chicago: University of Chicago Press, p. 195.
Engel, C and K D West (2005),” Exchange rates and fundamentals”, Journal of Political Economy 113(3): 485-517.
Gali, J and T Monacelli (2005), “Monetary policy and exchange rate volatility in a small open economy”, Review of Economic Studies 72(3): 707-734.
Justiniano, A and B Preston (2010a), “Can structural small-open economy models account for the influence of foreign disturbances?”, Journal of International Economics 81(1): 61-74.
Justiniano, A and B Preston (2010b), “Monetary policy and uncertainty in an empirical small-open economy model”, Journal of Applied Econometrics 25(1): 93-128.
Rogoff, K (1996), “The PPP puzzle”, Journal of Economic Literature 34(2): 647-668.
Rossi, B (2013), “Are exchange rates predictable?”, VoxEU.org, 14 November.