Over the last couple of years many central banks, for instance the ECB, the Federal Reserve Board, and Sveriges Riksbank, have started to build and estimate dynamic stochastic general equilibrium (DSGE) models, following the work by Christiano, Eichenbaum, and Evans (2005), and Smets and Wouters (2003). Sveriges Riksbank incorporated its open economy DSGE model, Ramses, into the daily process of forecasting and policy analysis in 2005; see Adolfson, Laséen, Lindé, and Villani (ALLV) (2007). Since Ramses is a structural model it can be used for policy analysis and policy simulation, but it also has good forecasting properties (ALLV 2008). In this column we discuss some practical policy considerations that need to be taken into account when using a DSGE model as a tool for policy analysis and forecasting.
Optimal policy projections
The way monetary policy is described in these modern DSGE models is often by a simple Taylor-type instrument rule (Taylor 1993), setting the instrument rate as a linear function of inflation and the output gap. The simple rule is then estimated (together with the rest of the model) based on historical data and hence for the historical conduct of monetary policy. However, policymakers may be more interested in knowing optimal policy projections of the future interest rate path rather than the path forecast from their predecessors’ handling of policy.
By optimal policy projections, we mean projections of the target variables (inflation and the output gap) and the instrument rate that minimise an intertemporal loss function corresponding to flexible inflation targeting, that is, a quadratic loss function of the gap between inflation and the inflation target and the gap between output and potential output (the loss function may or may not also include a term representing a preference for instrument-rate smoothing). Under optimal policy, the central bank responds to all relevant state variables and shocks, whereas with a simple rule the central bank only responds to a few key variables, such as inflation and the output gap. Therefore, optimal policy can more efficiently stabilise both inflation around the inflation target and the resource utilisation of the real economy, measured as the output gap.
Optimal policy consequently provides the efficient policy trade-offs between inflation and output-gap stabilisation that the policymaker faces. By varying the relative weight on output-gap stabilisation in the loss function, one obtains the set of efficient policy choices that the policymaker can choose between, which can give them useful advice for their decisions.
In our recent CEPR discussion paper, we provide a detailed analysis on how to do optimal policy projections in a linear-quadratic model with forward-looking variables. With these tools, we show that optimal policy projections can be carried out also in medium-sized DSGE models, like Ramses, and that this kind of analysis can now be applied in real-time policy processes.
Potential output
An important issue under flexible inflation targeting is which measure of the output gap policymakers should try to stabilise. In practice, central banks may look at different output gaps that measure deviations of actual output from different assessments of potential output. Stabilising different measures of potential output may result in different projections of the instrument rate.
In our paper we study several alternative definitions of potential output (and thereby the output gap) in our model. We define potential output as (i) trend output, the output level in a stochastic steady state or (ii) flexprice output, the hypothetical level of output that would prevail in the economy if nominal prices and wages were completely flexible. The second concept of potential output provides an important (equilibrium) benchmark to policy since it measures the level achievable if the central bank neutralises all nominal frictions in the economy. It differs from conventional (atheoretical) output-gap measures often used in empirical analysis, where potential output is computed using a smooth trend, for example, from a Hodrick-Prescott (HP) filter.
Furthermore, flexprice potential output can be defined in different ways depending on the assumption about the existing predetermined variables, such as the capital stock. We look at two different definitions: unconditional potential output is not contingent upon the current predetermined variables (the current state of the economy) but defined as the hypothetical output level that would result if prices and wages were completely flexible and had been so forever, whereas conditional potential output is conditional on the current state of the economy and is thus defined as the hypothetical output level that would arise if prices and wages suddenly became flexible in the current period and remained flexible in the future. In the first case, potential output depends on, for example, the hypothetical capital stock that would exist if prices and wages had been flexible forever; in the second case, potential output depends on the current capital stock (and therefore, to the extent the current capital stock depends on past policy, also on past policy).
Policy implications
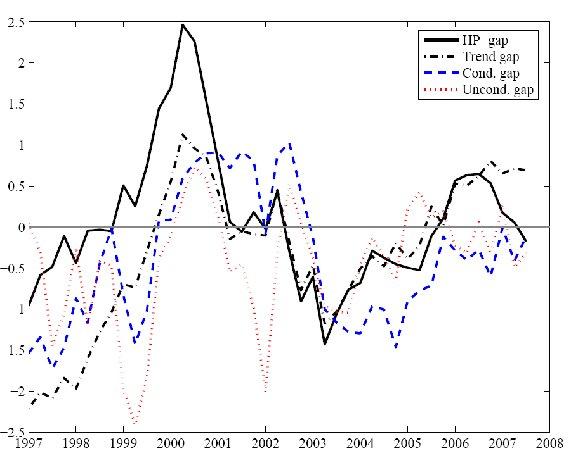
In Figure 1 we compare the various output gaps generated from the estimated DSGE model with an HP-filtered output gap in the data. We see that the historical development of the output gaps differ quite a bit. In certain years, such as 2006, the HP output gap and the trend output gap can even be of different sign than the two flexprice output gaps. This is because the model estimates a high temporary productivity shock during this year. This temporary productivity shock increases output but not trend potential output (since trend potential output is only affected by permanent (unit-root) shocks). Hence, the temporary productivity shock increases the trend output gap. In contrast, the temporary productivity shock increases the flexprice potential output, so since it increases both output and flexprice potential output, it will not increase the flexprice output gap. The different developments of the different output gaps will have policy implications. A central bank that stabilises the trend output gap will, for a positive temporary productivity shock, end up trying to reduce employment, but a central bank that stabilises the flexprice output gap will not.
Figure 1. Output gaps from the model and the data.
In our paper, we illustrate this by comparing optimal policy projections for different output gaps in the loss function and contrasting these with projections under the estimated instrument rule. We find that even if the response coefficients in the simple instrument rule and the parameters in the loss function are both estimated to reflect the historical behaviour of Sveriges Riksbank, the simple instrument rule and the optimal policy can generate quite different projections for inflation, output, and the instrument rate. The simple instrument rule is not at all as successful in keeping inflation close to the inflation target as the optimal policy. However, this does not necessarily require that monetary policy is always tighter under the optimal policy than under the simple instrument rule; this depends on the initial state of the economy. We also find that in situations when productivity is temporarily high, the optimal policy projections differ substantially depending on whether it is the flexprice or trend output gap that enters the loss function.
Model developments
Most of the DSGE models currently at use have a rather rudimentary description of the financial sector at work. This is also the case in our CEPR discussion paper. There is much recent research that can be used to incorporate various financial frictions (such as the role of collateral and borrowing constraints) into these models. It is not yet known whether this would improve the DSGE’s forecasting performance and how important financial factors are for replicating macroeconomic data and which role financial markets play in understanding business-cycle fluctuations.
Still, there are empirical indications that the current generation of DSGE models are misspecified (see, for example, Del Negro, Schorfheide, Smets and Wouters, 2007; ALLV 2008). This introduces another important challenge on how to formulate optimal monetary policy under model uncertainty.
Another field of criticism is that the contemporary DSGEs are linear rational-expectations models. Admittedly such models may be less suitable for describing financial crises or bubbles. Nevertheless, this type of DSGE model seems to be able to explain and forecast data quite well, which is essential for doing policy analysis. Having said that, there is promising work on DSGEs departing from the rational expectations assumption, for example, with agents updating their beliefs through learning (see Milani, 2007).
References
Adolfson, Malin, Stefan Laséen, Jesper Lindé, and Lars E.O. Svensson (2008), “Optimal Monetary Policy in an Operational Medium-Sized Model”, CEPR Discussion Paper No. 6907.
Adolfson, Malin, Stefan Laséen, Jesper Lindé, and Lars E.O. Svensson (2008), “Optimal Monetary Policy in an Operational Medium-Sized Model: Technical Appendix,”
Adolfson, Malin, Stefan Laséen, Jesper Lindé, and Mattias Villani (2007), “RAMSES — A New General Equilibrium Model for Monetary Policy Analysis,” Sveriges Riksbank Economic Review 2007:2, 5—39.
Adolfson, Malin, Stefan Laséen, Jesper Lindé, and Mattias Villani (2008), "Evaluating an Estimated New Keynesian Small Open Economy Model," Journal of Economic Dynamics and Control 32, 2690—2721.
Christiano, Lawrence, Martin Eichenbaum, and Charles Evans (2005), “Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy”, Journal of Political Economy 113(1), 1—45.
Del Negro Marco, Frank Schorfheide, Frank Smets, and Raf Wouters (2007), “On the Fit and Forecasting Performance of New Keynesian Models”, Journal of Business and Economic Statistics 25, 123-143.
Milani, Fabio (2007), “Expectations Learning and Macroeconomic Persistence”, Journal of Monetary Economics 54(7), 2065-2082.
Smets, Frank, and Raf Wouters (2003), “An Estimated Stochastic Dynamic General Equilibrium Model of the Euro Area”, Journal of the European Economic Association, 1(5), 1123-1175.
Taylor, John (1993), “Discretion Versus Policy Rules in Practice” Carnegie-Rochester Series on Public Policy, North-Holland, 39, 195—214.2007