Exchange rates are important contributors to business cycle fluctuations in open economies. Forecasting them, however, is not an easy task. Extensive literature stemming from the seminal work of Meese and Rogoff (1983) has established that a simple random walk generally delivers the most accurate point forecasts of exchange rates (see Rossi 2013 for a comprehensive review). This makes them uninteresting from an economic point of view, as future rates are just expected to be equal to current rates. In fact, models augmented with macroeconomic and financial fundamentals appear to improve random walk forecasts only at large horizons, though not systematically across exchange rates and samples. One explanation for this puzzling result is that the unpredictability of exchange rates might arise from the instability of their relationship with economic drivers.1
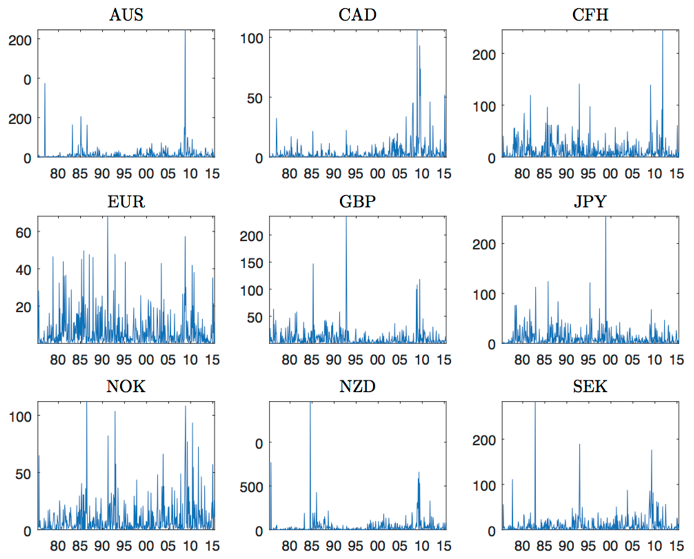
In a recent paper, we explore this hypothesis and assess the extent to which modelling parameter time variation in the effects of economic drivers improves the predictability of nine major currencies vis-a-vis the US dollar over the period 1976-2015 (the sample of currencies is selected to represent the set of G10 countries) (Abbate and Marcellino 2017). Figure 1 shows that the volatility of these exchange rates has varied greatly over time. It fell after the price shocks and inflationary pressures of the 1970s, and it increased again in the last decade, in conjunction with the crises in 2000-2001 and 2007-2008. Hence, a proper econometric model for forecasting exchange rates should also allow for changing volatility, as a constant volatility model could lead to incorrect forecast intervals, underestimating them in periods of high volatility and overestimating them otherwise.
Motivated by such considerations, we evaluate whether the point, interval, and density forecasts of each of the exchange rates in the sample can be improved by: (i) allowing for parameter time-variation in the slope and volatility parameters of the forecast models; and (ii) controlling for other currencies and for macroeconomic fundamentals such as cross-country differentials in interest rates, inflation, and output.2 Time variation is modelled through a forgetting factor VAR, recently proposed by Koop and Korobilis (2013), which is computationally tractable for medium-sized models, and exploits the information from current forecast errors to determine the extent of time variation.
Figure 1. Exchange rate volatility over the years, measured as the square monthly percentage changes in the exchange rate reported in the title (number of currency units per US dollar)
Delivering accurately calibrated interval forecasts
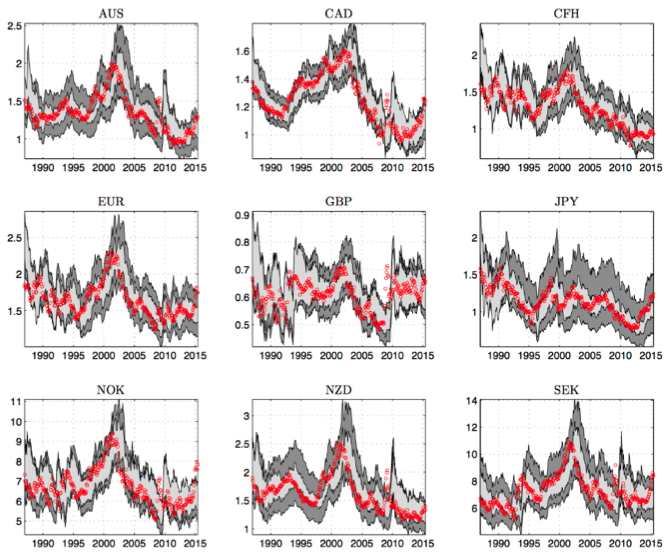
We find that modelling parameter time variation reduces the uncertainty around future exchange rates, though it does not systematically improve point forecasts. Time-varying parameter models deliver 68% and 95% forecast confidence intervals, which are on average accurately calibrated (according to unconditional coverage tests), meaning that on average they contain future exchange rates 68% and 95% of the time. Conversely, constant-parameter models generate forecast confidence intervals which are excessively large. This is best exemplified by Figure 2, where we show actual exchange rates (red dotted lines) along with the 68% forecast confidence intervals at a one-year horizon from a random walk (dark grey area) and from a time-varying autoregressive model (light grey area). Results from time-varying VAR models with and without fundamentals are very similar. The forecast confidence intervals of the time-varying models are narrower, and contain the actual exchange rates with the expected rate.
Moreover, we find that modelling parameter time variation is better suited to long horizons and periods of high volatility, especially in the decade between 2000 and 2010. The largest forecast improvements come, in fact, from modelling time variation in the volatilities of the innovations, rather than in the slope parameters of the VAR.
Figure 2. Forecast confidence intervals
Note: 68% forecast confidence intervals delivered by the random walk (dark grey area) and by the time-varying autoregressive model (light grey area) at a one-year horizon. Dotted red lines denote actual exchange rate levels. Time-varying parameter models deliver 68% and 95% forecast confidence intervals which are on average accurately calibrated, while constant-parameter models generate forecast confidence intervals which are excessively large.
The information provided by macroeconomic fundamentals has economic value
Another feature emerging from Figure 2 is that, naturally, there is substantial uncertainty around future exchange rates, even when using proper econometric models. This raises the question of the overall usefulness of exchange rates forecasts. To try to answer this question, we build trading strategies based on the competing forecast models, taking the perspective of a US investor with a one-month trading horizon. The analysis reveals an economic value of controlling for both parameter time variation, and for the informational content provided by other currencies and by macroeconomic fundamentals. Controlling for the latter in a time-varying parameter model with changing volatilities yields the highest portfolio returns across all competing strategies.3
Conclusions
Modelling time variation in the cross-rate relationships, and in the volatilities of the shocks hitting the economic system, significantly improves exchange rates forecasts. In fact, the more sophisticated econometric models deliver forecast confidence intervals that are on average accurately calibrated, and they appear to perform particularly well in high-volatility periods.
Moreover, trading strategies based on the different forecast models show that controlling for parameter time variation and for macroeconomic fundamentals leads to higher portfolio returns, and to higher values for investors. Hence, allowing for parameter time variation reveals an economic value of the information provided by macroeconomic fundamentals, though it is not needed for the fundamentals to show predictive content at larger horizons.
References
Abbate, A, and M Marcellino (2017), “Point, interval and density forecasts of exchange rate with time-varying parameter models”, CEPR Discussion Paper no. 11559, forthcoming in the Journal of Royal Statistical Society, Series A.
Cheung, Y-W, and M D Chinn (2001), “Currency traders and exchange rate dynamics: a survey of the US market”, Journal of International Money and Finance, 20 (4):439–471.
Della Corte, P, L Sarno, and I Tsiakas (2009), “An economic evaluation of empirical exchange rate models”, Review of Financial Studies, 22 (9): 3491–3530.
Koop, G, and D Korobilis (2013), “Large time-varying parameter VARs”, Journal of Econometrics, 177: 185–198.
Meese, R, and K Rogoff (1983), “The out-of-sample failure of empirical exchange rate models: Sampling error or misspecification?” In Exchange Rates and International Macroeconomics, NBER Chapters, 67–112.
Rossi, B (2013), “Exchange rate predictability”, Journal of Economic Literature, 51 (4).
Rossi, B (2006), “Are exchange rates really random walks? Some evidence robust to parameter instability”, Macroeconomic Dynamics, 10 (1): 20–38.
Endnotes
[1] For example, see the evidence provided by Rossi (2006). Moreover, instability may arise from trading strategies that involve frequent changes to the weight attached to fundamentals, as documented through survey evidence by Cheung and Chinn (2001).
[2] These macroeconomic fundamentals are typically indicated in the economic literature as potential drivers of exchange rates. See Section 2 of Abbate and Marcellino (2017) for a more thorough discussion.
[3] This result is confirmed by using a wide range of performance criteria, including performance fees and breakeven transaction costs. We refer to Section 5 of Abbate and Marcellino (2017), as well as to Della Corte et al. (2009) for more results and a thorough discussion.