Population agglomeration is a manifest and global trend. If it is identified by the set of contiguous areas with population density of at least 1,000 people per km2 and total population of at least 10,000,1 such areas accounted for 44.6% (1.6%), 43.6% (2.4%), 48.7% (2.9%), 47.0% (3.8%) and 77.1% (12.4%) of the total population (area) in Europe, the US, China and India, and Japan, respectively, in 2015. While the case of Japan is exceptional due to its relative scarcity of land, the disproportionate concentration of population appears to be a ubiquitous phenomenon across the world. Thus, it is natural to view economic geography in terms of the system of (economic) cities.
Substantial evidence (e.g. Bettencourt et al. 2007) has indicated strong correlations between socioeconomic quantities and population sizes of cities (e.g. wages, GDP, number of patents produced for positive correlations, amount of crime, and the level of traffic congestion for negative correlations). As such, it is of particular interest to know and explain where and what sizes of cities form, and which cities grow or decline.
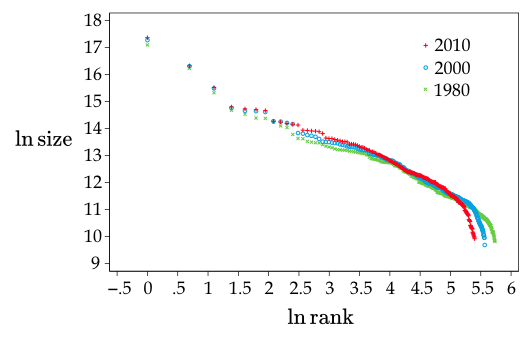
It is well known that a city size distribution in a relatively autonomous economic region – typically a country or a fairly integrated set of contiguous countries such as the EU – approximately follows a (region-specific) power law (e.g. Decker et al. 2007). Figure 1 shows the rank-(population) size distributions of cities in Japan in 1980, 2000, and 2010 (where the rank indicates the ranking in terms of population size).2 Throughout the 30-year period, the upper tail of the city size distribution maintains a fairly persistent power law.
Figure 1 Rank-size distribution of cities in Japan
Population sizes of cities are highly indicative of their industrial structure. In recent research, for each of the 110 three-digit manufacturing industries that appear consistently from 1980 to 2010, I identified the cities in which each industry has significant agglomeration, designated as agglomeration cities of this industry (Mori 2017).3 I show that the number and average population size of the agglomeration cities of an industry exhibit a sharp and persistent log-linear relationship, as shown in Figure 2 for 1980, 2000, and 2010.
Figure 2 Number and average size of agglomeration cities of manufacturing industries in Japan
As is evident from the figure, the number of agglomeration cities differ widely across industries, and the industries that are located in a smaller number of cities are found in larger cities. Indeed, these industries exhibit a strong spatial coordination of agglomerations – cities that have more localised industries also contain more ubiquitous ones. Consequently, there is a hierarchical relation in the industrial composition between larger and smaller cities.
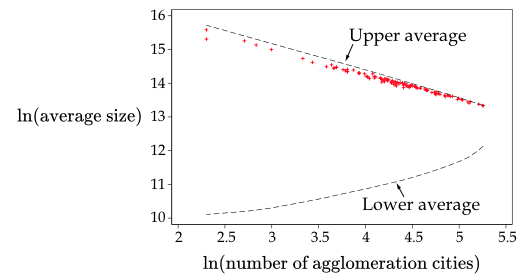
To see this hierarchical structure more clearly, Figure 3 re-plots the number and average size of agglomeration cities of industries in 2010 (in red), together with their upper and lower bounds (dashed curves).4 Provided that the red plots can only locate between the two dashed curves, one can see that the realised average sizes of agglomeration cities are almost hitting their upper bound, which means essentially that the industries are agglomerating in the largest cities.5
Figure 3 Upper and lower bounds for the average size of agglomeration cities
A further intriguing fact is that behind these strong and persistent power law regularities exhibited by population and industrial agglomeration patterns, there is considerable churning of population and industrial activities among cities. On the one hand, of the 309 cities that existed in 1980, 114 either were absorbed into other cities or simply disappeared, while 26 were newly formed, leaving 221 in 2010. The cities that were present in both 1980 and 2010 experienced a 24% population growth on average with a standard deviation as large as 47% (where the total population has grown by 9%). On the other hand, there is also substantial churning of industries among cities. While there is high correlation of 0.94 between the industrial diversity (as defined by the number of industries agglomerated) in a city in 1980 and that in 2010,6 the industrial composition of an individual city has changed by more than 30% on average.7
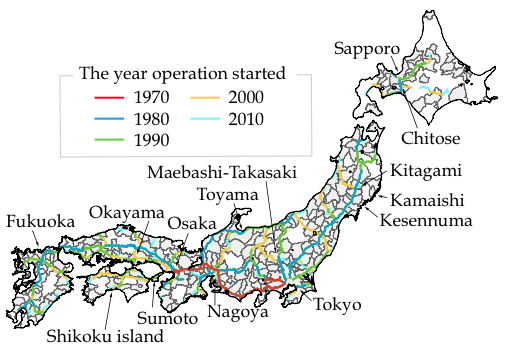
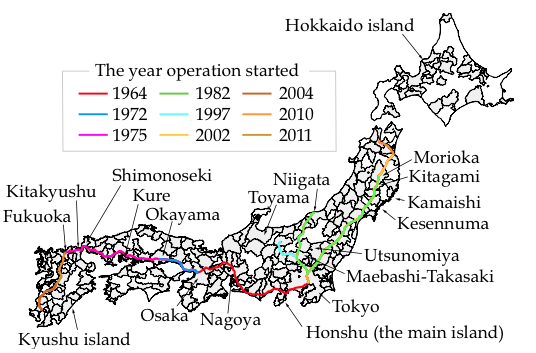
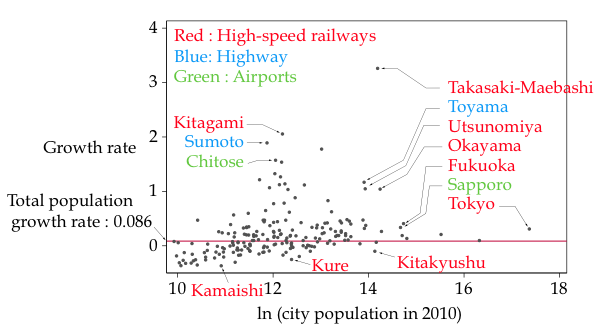
For the case of Japan, the large variation in the population growth of cities clearly reflects the development of highway and high-speed railway networks (Figures 4 and 5, respectively) that started in the 1960s and were almost completed by 2010. Figure 6 plots the population growth rates (between 1980 and 2010) of cities that existed in both 1980 and 2010, where the cities whose growth/decline were strongly influenced by the development of highways, high-speed railways, and airports are indicated in blue, red, and green, respectively.
Figure 4 Development of the highway network in Japan
Figure 5 Development of the high-speed railway network in Japan
Figure 6 Population growth of cities between 1980 and 2010
One can see that the large deviations (both positive and negative) are often related to transport network development. In particular, those that are located directly at the major terminals and intersections have grown substantially (e.g. Tokyo, Fukuoka, Okayama, Sapporo), while those that are isolated from the network development have declined substantially (e.g. Kamaishi, Kesennuma). However, a generally overlooked fact is that an improvement in interregional access at a given city location does not by itself necessarily result in the population growth of that city, if this city were located in the vicinity of other major cities – especially those at the major transport nodes. For example, Kitakyushu located right next to Fukuoka, and Kure located between Fukuoka and Okayama (refer to Figure 5) experienced substantial decline in population despite being on the same major highway and high-speed railway routes as Fukuoka and Okayama. This negative impact of improved interregional transport access is due to the presence of an agglomeration shadow of nearby major cities.
These facts have an important policy implication. Although there is room for influencing the sizes and socioeconomic structures of individual cities by regional policies – as transport development policies appear to have an obvious impact as demonstrated above – there is also a system-level ‘musical chair’ constraint, in that the number and spacing of cities that can grow are subject to those stringent power law regularities. In particular, uniform improvement of transport access (such as the nationwide development of highways) does not have a monotonic impact on the growth of individual cities and regions, as there are only a limited number of ‘chairs’ for cities/regions to grow.
These distributional constraints of economic agglomeration have been mostly neglected in the extant empirical and policy literature on the economic agglomerations (see for example Redding and Turner 2015 for a survey), and the growth of an individual city/region usually is related to its local characteristics (e.g. interregional transport access). This is perhaps one of the most urgent aspects of economic agglomeration to be explicitly taken into account in both theoretical and empirical analyses (see Akamatsu et al. 2017 for extensive discussion on both theoretical and empirical frameworks in this direction).
Editor's Note: The main research on which this column is based first appeared as a Discussion Paper of the Research Institute of Economy, Trade and Industry (RIETI) of Japan.
References
Akamatsu, T, T Mori, M Osawa, and Y Takayama (2017), “Spatial scale of agglomeration and dispersion: Theoretical foundations and empirical implications”, Discussion paper No. 80689, Munich Personal RePEc Archives.
Bettencourt, L M A, J Lobo, D Helbing, C Kühnert, and G B West (2007), “Growth, innovation, scaling and the pace of life in cities”, Proceedings of the National Academy of Sciences, 104 (17), 7301-7306.
Decker, E H, A J Kerkhoff, and M E Moses (2007), “Global patterns of city size distributions and their fundamental drivers”, PLoS ONE 2 (9), e934.
Kanemoto, Y, and K Tokuoka (2001), “Proposal for the standards of metropolitan areas of Japan (in Japanese),” Journal of Applied Regional Science, 7, 1-15.
Mori, T (2017), “Evolution of sizes and industrial structure of cities in Japan from 1980 to 2010: Constant churning and persistent regularity,” Asian Development Review, forthcoming.
Mori, T, and T E Smith (2014), “A probabilistic modeling approach to the detection of industrial agglomerations”, Journal of Economic Geography, 14 (3), 547-588.
Redding, S J, and M A Turner (2015), “Transport costs and the spatial organization of economic activity,” in G Duranton, J V Henderson, and W C Strange (eds.), Handbook of Regional and Urban Economics vol. 5, Elsevier: 1339-1398.
Endnotes
[1] The computation is based on the estimated ambient population count at the 30″×30″ grid level obtained from the LandScan data developed by Oak Ridge National Laboratory for Europe, the US, China, and India. The corresponding data for Japan is based on the Population Census of Japan in 2015.
[2] The definition of a city here is based on the Urban Employment Area by Kanemoto and Tokuoka (2001).
[3] Industrial agglomerations are identified using statistical clustering technique developed by Mori and Smith (2014).
[4] For each number n of agglomeration cities (along the horizontal axis), the upper (lower) bound is given by the average size of the largest (smallest) n cities.
[5] The hierarchy of industrial composition of cities together with power law for city size distributions were first formally explained by Hsu (2012) by means of an endogenous agglomeration mechanism arising from the presence of transport costs and a large diversity in increasing returns.
[6] Here, the city boundaries are fixed to those as of 2010 to make comparison of industrial composition of each city between 1980 and 2010.
[7] Comparison of industrial composition of a given city between 1980 and 2010 is based on the Jaccar index, which is defined by the share of the intersection over the union of the set of industries agglomerated in this city in 1980 and that in 2010. The average index value among the 110 manufacturing industries is 0.52. For a given level of industrial diversity, a Jaccar index of 0.5 means the replacement of one-third of industries in this city.