Government statistical agencies commonly report official economic statistics as point estimates. Agency documents describing data and methods may acknowledge that estimates are subject to error, but they typically do not quantify error magnitudes. News releases present estimates with little if any mention of potential error.
In the absence of agency guidance, users of official statistics may misinterpret the information that the statistics provide. I urge statistical agencies to measure uncertainty and report it in their news releases and technical publications.
Why is it important to communicate uncertainty in official statistics? A broad reason is that governments, firms, and individuals use the statistics when making numerous decisions. The quality of decisions may suffer if decision makers incorrectly take reported statistics at face value or incorrectly conjecture error magnitudes. For example, a central bank may mis-evaluate the status of the economy and consequently set inappropriate monetary policy (Lindé et al. 2008). Agency communication of uncertainty would enable decision makers to better understand the information actually available regarding key economic variables.
Sampling error for statistics based on survey data can be measured using established statistical principles. The challenge is to satisfactorily measure nonsampling error. There are many sources of such errors and there has been no consensus about how to measure them. I find it useful to distinguish transitory statistical uncertainty, permanent statistical uncertainty, and conceptual uncertainty.
Transitory statistical uncertainty arises because data collection takes time. Agencies sometimes release a preliminary estimate of an official statistic in an early stage of data collection and revise the estimate as new data arrive. Hence, uncertainty may be substantial early on but diminish as data accumulate.
Permanent statistical uncertainty arises from incompleteness or inadequacy of data collection that does not diminish with time. In survey research, considerable permanent uncertainty may stem from non-response and from the possibility that some respondents may provide inaccurate data.
Conceptual uncertainty arises from incomplete understanding of the information that official statistics provide about well-defined economic concepts or from lack of clarity in the concepts themselves. Thus, conceptual uncertainty concerns the interpretation of statistics rather than their magnitudes.
This column, which summarises material from Manski (2014), illustrates each form of uncertainty and discusses strategies for measurement and communication.
Transitory Uncertainty in National Income Accounts
In the United States, the Bureau of Economic Analysis (BEA) reports multiple vintages of quarterly GDP estimates. An advance estimate combines data available one month after the end of a quarter with trend extrapolations. Second and third estimates are released after two and three months, when new data become available. A first annual estimate is released in the summer, based on more extensive data collected annually. There are subsequent annual and five-year revisions.
BEA analysts have provided an upbeat perspective on the accuracy of GDP statistics. Landefeld, Seskin, and Fraumeni (2008) state (p. 213): “In terms of international comparisons, the U.S. national accounts meet or exceed internationally accepted levels of accuracy and comparability. The US real GDP estimates appear to be at least as accurate (based on a comparison of GDP revisions across countries) as the corresponding estimates from other major developed countries.”
Croushore (2011) offers a considerably more cautionary perspective (p. 73): “Until recently, macroeconomists assumed that data revisions were small and random and thus had no effect on structural modelling, policy analysis, or forecasting. But real time research has shown that this assumption is false and that data revisions matter in many unexpected ways.”
Measurement of transitory uncertainty in GDP estimates is straightforward if it is credible to assume that the revision process is time-stationary. Then, historical data on revisions can be extrapolated to measure the uncertainty of future revisions. A simple extrapolation would be to suppose that the empirical distribution of revisions will persist.
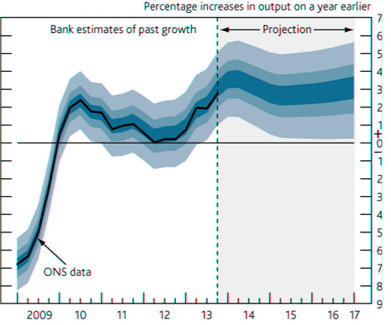
A notable precedent is the regular release of fan charts by the Bank of England. The figure below reproduces a fan chart for annual GDP growth in the February 2014 Inflation Report (Bank of England 2014). The part of the plot showing growth from late 2013 on is a probabilistic forecast that expresses the uncertainty of the Bank’s Monetary Policy Committee regarding future GDP growth. The part showing growth in the period 2009 through mid 2013 is a probabilistic forecast that expresses uncertainty regarding the revisions that the UK Office of National Statistics will henceforth make to its estimates of past GDP. The Bank explains as follows (p. 7): “In the GDP fan chart, the distribution to the left of the vertical dashed line reflects the likelihood of revisions to the data over the past.”
Observe that the figure expresses considerable uncertainty about GDP growth in the period 2010-2013. Thus, the Bank judges that future revisions to estimates of past GDP may be large in magnitude.
Figure 1. Fan chart for annual GDP growth
Source: Bank of England (2014)
Permanent uncertainty due to survey non-response
Each year the United States Census Bureau reports statistics on the household income distribution based on income data collected in a supplement to the Current Population Survey (CPS). There is considerable non-response. During 2002-2012, 7 to 9% of the sampled households yielded no income data due to unit non-response, and 41 to 47% of the interviewed households yielded incomplete income data due to item non-response (Manski 2013). Nevertheless, Census publications give the impression that statistics on the income distribution are exact.
To produce point estimates, the Census Bureau applies hot-deck imputations, stating (U. S. Census Bureau 2006, p. 9-2): “This method assigns a missing value from a record with similar characteristics, which is the hot deck. Hot decks are defined by variables such as age, race, and sex. Other characteristics used in hot decks vary depending on the nature of the unanswered question. For instance, most labour force questions use age, race, sex, and occasionally another correlated labour force item such as full- or part-time status.”
CPS documentation offers no evidence that the hot-deck method yields a distribution for missing data that is close to the actual distribution. Another Census document describing the American Housing Survey is revealing (US Census Bureau 2011, p. D-2): “Some people refuse the interview or do not know the answers. When the entire interview is missing, other similar interviews represent the missing ones [...] For most missing answers, an answer from a similar household is copied. The Census Bureau does not know how close the imputed values are to the actual values.”
Econometric research has shown how to measure uncertainty due to non-response without making assumptions about the nature of the missing data. One contemplates all values that the missing data can take. Then, the data yield interval estimates of official statistics. The literature derives these intervals for population means, quantiles, and other parameters (Manski 2007, Chapter 2). The literature also shows how to form confidence intervals that jointly measure sampling and non-response error (Imbens and Manski 2004).
To illustrate, I have used CPS data to form interval estimates of median household income and the fraction of families with income below the poverty line in 2001-2011 (Manski 2013). One set of estimates takes into account item non-response alone, and another recognises unit response as well. The estimates show that item non-response poses a huge potential problem for inference on the American income distribution. Unit non-response exacerbates the problem.
Conceptual uncertainty in seasonal adjustment
Viewed from a sufficiently high altitude, the purpose of seasonal adjustment of official statistics appears straightforward. The US Bureau of Labour Statistics explains seasonal adjustment of employment statistics this way (US Bureau of Labour Statistics 2001): “What is seasonal adjustment? Seasonal adjustment is a statistical technique that attempts to measure and remove the influences of predictable seasonal patterns to reveal how employment and unemployment change from month to month.”
It is less clear from ground level how one should actually perform seasonal adjustment. Statistical agencies in the US use the X-12-ARIMA method (Findley et al. 1998). X-12 may be a sophisticated and successful algorithm. Or it may be an unfathomable black box containing a complex set of statistical operations that lack economic foundation. Wright (2013) expresses the difficulty of understanding X-12 this way (p. 2): “Most academics treat seasonal adjustment as a very mundane job, rumoured to be undertaken by hobbits living in holes in the ground. I believe that this is a terrible mistake.” He goes on to say that “Seasonal adjustment is extraordinarily consequential.”
There now exists no clearly appropriate way to measure the uncertainty associated with seasonal adjustment. X-12 is a standalone algorithm, not a method based on a well-specified dynamic theory of the economy. It is not obvious how to evaluate the extent to which it accomplishes the objective of removing the influences of predictable seasonal patterns. One might perhaps juxtapose X-12 with other proposed algorithms, perform seasonal adjustment with each one, and view the range of resulting estimates as a measure of conceptual uncertainty.
A more radical departure from current practice would be to abandon seasonal adjustment and leave it to the users of official statistics to interpret unadjusted statistics as they choose. Analysis of unadjusted statistics should be particularly valuable to users who want to assess the economy on an annual rather than monthly basis. Suppose, for example, that one wants to compare unemployment in March 2013 and March 2014. It is arguably more reasonable to compare the unadjusted estimates for these months than to compare the seasonally adjusted estimates. The unadjusted estimates are comprised of data actually collected in the two months of interest. In contrast, the seasonally adjusted estimates for March 2013 and March 2014 are comprised of data collected not only in these months but over a lengthy prior period.
Conclusion
I have suggested ways to measure the transitory statistical uncertainty in estimates of official statistics based on incomplete data and the permanent statistical uncertainty stemming from survey non-response. I have also called attention to the conceptual uncertainty in seasonal adjustment. Statistical agencies would better inform policymakers and the public if they were to measure and communicate these and other significant uncertainties in official statistics. I urge them to do so.
An open question is how communication of uncertainty would affect policymaking and private decision making. We now have little understanding of the ways that users of official statistics interpret them. Nor do we know how decision making would change if statistical agencies were to communicate uncertainty regularly and transparently. I urge behavioural and social scientists to initiate empirical studies that would shed light on these matters.
References
Bank of England (2014), Inflation Report Fan Charts February 2014, accessed April 26, 2014.
Croushore, D. (2011), "Frontiers of Real-Time Data Analysis," Journal of Economic Literature, 49, 72-100.
Findley, D., B. Monsell, W. Bell, M. Otto and B. Chen (1998), "New Capabilities and Methods of the X-12-ARIMA Seasonal-Adjustment Program," Journal of Business & Economic Statistics, 16, 127-152.
Imbens, G. and C. Manski (2004), "Confidence Intervals for Partially Identified Parameters," Econometrica, 72, 1845B1857.
Landefeld, J., E. Seskin, and B. Fraumeni (2008), "Taking the Pulse of the Economy: Measuring GDP," Journal of Economic Perspectives, 22, 193-216.
Lindé, Jesper , Lars E.O. Svensson, Stefan Laséen, and Malin Adolfson (2008), “Can optimal policy projections in DSGE models be useful for policymakers?”, VoxEU.org, 16 September
Manski, C. (2007), Identification for Prediction and Decision, Cambridge: Harvard University Press.
Manski, C. (2013), "Credible Interval Estimates for Official Statistics with Survey Nonresponse," Department of Economics, Northwestern University.
Manski, C. (2014), "Communicating Uncertainty in Official Economic Statistics," National Bureau of Economic Research Working Paper 20098.
U. S. Bureau of Labor Statistics (2001), Labor Force Statistics from the Current Population Survey, accessed April 26, 2014.
U. S. Census Bureau (2006), Current Population Survey Design and Methodology, Technical Paper 66, Washington, DC: U. S. Census Bureau.
U.S. Census Bureau (2011), Current Housing Reports, Series H150/09, American Housing Survey for the United States: 2009, Washington, DC: U.S. Government Printing Office.
Wright, J. (2013), "Unseasonal Seasonals?" Department of Economics, Johns Hopkins University.