Economists are used to thinking about individual decisions under risk and how these affect aggregate outcomes. The decision to socialise, go for a haircut or to a yoga class, work from home or use public transport will ultimate determine how often people come in contact with each other and therefore how easy it is for infections to get transmitted. Social distancing, which has been elevated to paramount importance for the mitigation of the current coronavirus epidemic, fits very well in the analytical frameworks in which economists specialise. Therefore, economists can have a role to play in the design of lockdown policies for the current Covid-19 epidemic, alongside epidemiologists and other natural scientists.1 In this column, we will highlight how standard economic reasoning about (strategic) interactions between individuals can be fruitfully integrated in an epidemiological model that has been commonly used to guide policy advice in the current coronavirus crisis.
The most famous epidemiological model is the SIR model, developed in 1927. The first modelling assumption is that the population can be classified into three pools – Susceptible to infection, Infectious, and Recovered – where the latter is the part of the population that consists of all individuals who are neither infectious nor susceptible to infection (for example, because they have become immune). S is the proportion in the population of susceptible individuals. The ‘basic reproduction number’, R0, is the mean number of infections directly generated by one case if all individuals were susceptible to infection and could come in contact with the infected person. R0 measures the maximum reproductive potential for an infectious disease. With no restrictions in contacts, the ‘effective reproduction number’ is R0 times S, which gives the number of infections produced by an infectious person. If the effective reproduction number is greater than one, then infections will grow given the prevailing level of ‘herd immunity’, 1-S. As infections grow, the pool of susceptible individuals becomes smaller, the effective reproduction number eventually drops below one and infections start decreasing, vanishing towards the end of the epidemic.
This simple model can be extended in various directions to better fit what we currently know about Covid-19, thus improving its predictive power. For instance, it can be extended to include ‘high-risk’ individuals who develop a serious illness because of the infection, and ‘low-risk’ individuals who only have mild or moderate symptoms. It can also accommodate for a proportion of the high-risk population dying (after some days). This ‘mortality rate’ can also be higher the higher the share of the high-risk population that is infected, capturing limited resources available for the effective health care of high-risk individuals. Some terminally ill individuals may also stop being infectious due to their hospitalisation, or will remain infectious if they are unable to leave their family home, hospice, etc.
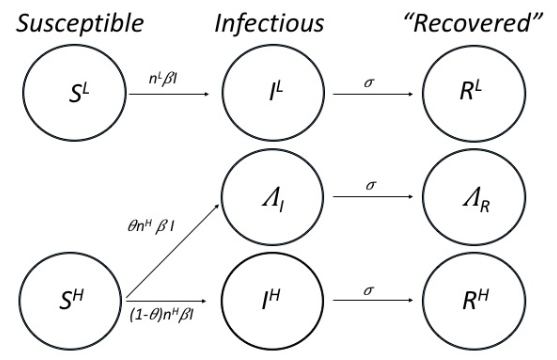
The model can also be extended to take into account that individuals may come in contact only with some people, with their contact rate possibly being dependent on whether or not they are at high risk of developing a serious illness. There are more extensions that one could think of,2 but this extended SIR model is a good approximation of the Covid-19 epidemic and one of the workhorses of policy analysis for tackling the current crisis.3 Figure 1 provides a diagrammatic representation of this extended SIR model.
‘Gamma’ is the implied mean contact rate in this extended SIR model. The effective reproduction number becomes gamma times R0 times S. This number must be below one for an infection to not set off (given the prevailing level of herd immunity, 1-S). This inequality forms the basis of arguments in favour of strict lockdowns (a low gamma), high ‘herd immunity’ (a low S), or testing and tracing (a low basic reproduction number) to avoid a second wave of infections.
Figure 1 The states and flows of the extended SIR model
Notes: Circles depict pools of individuals (as proportions in the population) and arrows depict flows between states. Transition rates between states are given next to the corresponding arrows. SH, IH and RH are the pools of high-risk susceptible, infectious and recovered individuals, respectively. SL, IL and RL are the pools of low-risk susceptible, infectious and recovered individuals, respectively. I is the pool of the terminally-ill high-risk individuals who are infectious. R is the pool of the terminally-ill high-risk individuals who do not contribute to the spread of the infection (due to hospitalization). SL and SH comprise S. IL, IH and I comprise I.RL, RH and R comprise R. is the mean number of infections per unit of time when every person is susceptible, is rate at which infectious individuals stop contributing to the spread of the infection, and hence the basic reproduction number is R0 = /. The mortality rate of the high-risk infected individuals is . In addition, nH is the contact rate of high-risk individuals, and nL the contact rate of low-risk individuals. The mean contact rate in this model is equal to (1-)nL+nH, where denotes the proportion in the population of the high-risk individuals.
However, the above model does not take into account that (1) individuals make decisions to socially distance even in the absence of government interventions; and (2) people may respond behaviourally to government interventions that aim at influencing the evolution of the current epidemic. The reason for the latter is that the proportion of infectious people in the population will determine the probability that a susceptible person will get infected, as well as the probability that a high-risk individual will die after being infected. Therefore, decisions on social distancing will naturally depend, among other things, on personal health conditions and government policy. Ignoring this may be an important shortcoming because the mean contact rate might actually change over time or following a change in government policy, with unintended consequences. In a nutshell, the mean contact rate cannot be treated separately from the level of herd immunity when policy focuses on bringing the effective reproduction number below one.
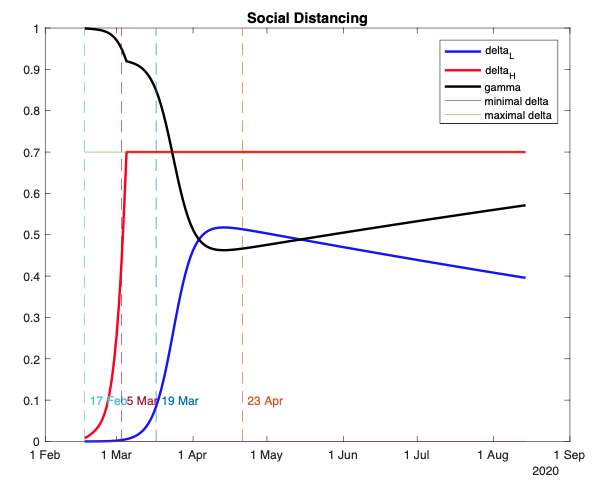
In a work in progress Makris (2020), I build a model that addresses this shortcoming.4 In this model, individuals perceive themselves as unable to affect the overall evolution of the epidemic and the mean contact rate. Individuals choose their own social distancing, ‘delta’, which is defined as the proportion of severed contacts – that is, an individual’s contact rate is equal to one minus delta. Social distancing must be between some lower bound (the ‘minimal’ degree of social distancing) and some upper bound (the ‘maximal’ degree of social distancing). The minimal social distancing is zero in the absence of a government lockdown policy. The maximal social distancing will depend on the relative size of the ‘essential’ sectors in the economy or on which types of contact are feasible. In equilibrium, the mean contact rate is equal to the actual mean contact rate that is implied by private decisions. In the absence of an altruistic motive,5 non-susceptible individuals choose the minimal social distancing and low-risk individuals choose to exercise some social distancing throughout the epidemic, whereas high-risk individuals will exercise much stricter social distancing, reaching maximal social distancing before the infection peaks and maintaining it for some time after the infection peaks (see Figure 2).
As a result, lockdown policies that shut down non-essential sectors (e.g. services) and thereby increase the minimal level of social distancing will influence mostly the behaviour of (non-susceptible and) low-risk susceptible individuals, whereas policies that shut down some of the less essential sectors (e.g. parts of government services or the food industry) and thereby increase the maximal level of social distancing will influence mostly the behaviour of high-risk susceptible people.
Consequently, different types of lockdown policies will influence different dimensions of the epidemic. For instance, policies that increase the maximal level of social distancing have a much stronger impact on the death toll than on the evolution of infections and the level of ‘herd immunity’ compared to the effects of policies that increase the minimal level of social distancing.
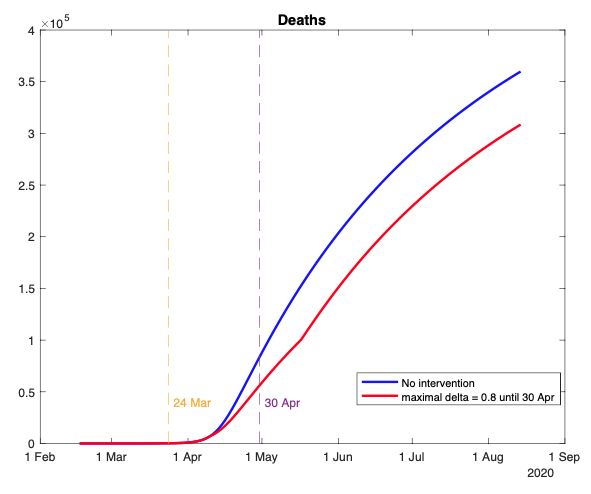
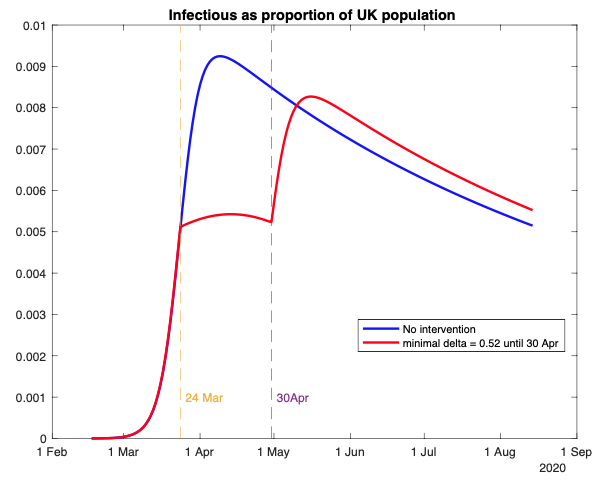
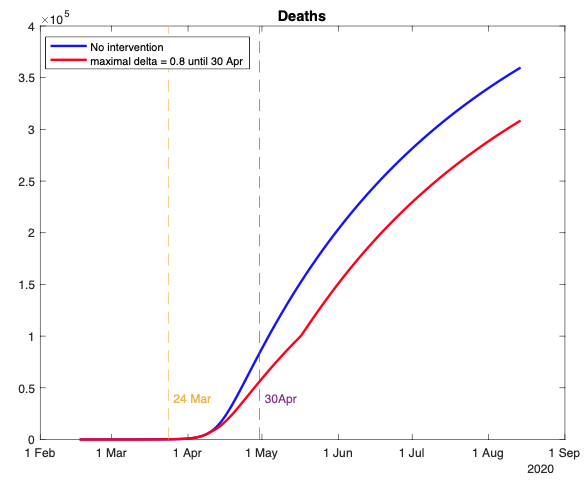
Figure 3 shows the result on the death count of raising the maximal social distancing from 0.7 to 0.8 (i.e. shutting down one third of the less essential sectors); Figures 4 to 6 show the result on the pool of infectious, the pool of exposed (infectious and recovered) people and on the death toll, respectively, of raising the minimal social distancing from zero to 0.52 (i.e. shutting down non-essential sectors that comprise around 52% of the economy). Both examples of lockdown policies last for five weeks starting on 24 March (the actual date of the UK lockdown).
Figure 2
Notes: The figure demonstrates the equilibrium social distancing and mean contact rate when the basic reproduction number is R0=2.25, the rate of recovery is s=1/4.5, and there are 17 days on average between the onset of illness and death. These values have also been used in Lourenço et. al. (2020). Moreover, the proportion of high-risk individuals in the population is =0.1044. This value is derived through the calibration of our model. The minimal social distancing is zero and the maximal social distancing is 0.7. We also use the assumptions that there is no mutation, not testing and no vaccine in the following few months. The social distancing of non-susceptible people is equal to the minimal social distancing. Vertical lines indicate the following dates. 5 Mar is the date the first UK death was reported, and 19 Mar. 5 Mar-15 Apr is the 15-days window we used for the calibration of our model to avoid the effects of any mitigation policies. 17 Feb is 17 days before the date the first UK death was reported. Given the mean time length from the onset of the illness to death of 17 days, we used 17 Feb as the first date of the infection (the “introduction date”).
Figure 3
Notes: Cumulative deaths under no intervention (blue line) and an intervention (red line) that raises maximal social distancing from 0.7 to 0.8 for the period 24 March to 30 April 2020. Otherwise, the underlying model is as in Figure 2.
Figure 4
Notes: Percentage of the UK population of Infectious people under no intervention (blue line) and an intervention (red line) that raises minimal social distancing from 0 to 0.52 for the period 24 March to 30 April 2020. Otherwise, the underlying model is as in Figure 2.
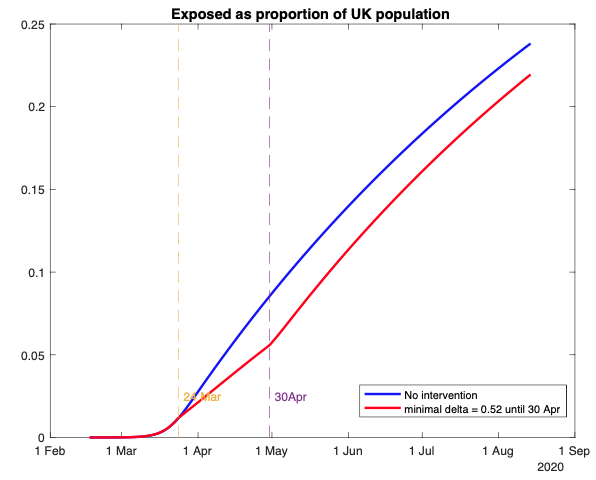
Figure 5
Notes: Percentage of the UK population of exposed (infectious and recovered) people under no intervention (blue line) and an intervention (red line) that raises minimal social distancing from 0 to 0.52 for the period 24 March to 30 April 2020. Otherwise, the underlying model is as in Figure 2.
Figure 6
Notes: Cumulative deaths under no intervention (blue line) and an intervention (red line) that raises minimal social distancing from 0 to 0.52 for the period 24/03-30/04/2020. Otherwise, the underlying model is as in Figure 2.
This previously unrecognised interaction between private decisions in an heterogenous population, government interventions, and the evolution of an epidemic raises the need to investigate quantitatively the predictions of our ‘equilibrium SIR model’. To this end, we calibrate our model to UK data on reported deaths during the first 15 days from the date the first death was reported (i.e. 05 March to 19 March) to avoid any effect of mitigating interventions.6 Initial simulations that are only meant to highlight the importance of incorporating endogenous social distancing in an heterogenous population suggest the following predictions.7
- By the date of the first reported death, around 0.02% of the UK population would have already been exposed to the virus.8
- The peak of the mortality rate would have occurred around the beginning of the second week of April in the absence of government intervention, but with a significant death toll by the end of the epidemic of around 574,000 people.
- Policies that raise the minimal level of social distancing (e.g. a reduction in contact rate by 52%) lead to a ‘flattening of the infection curve’ during the intervention period.
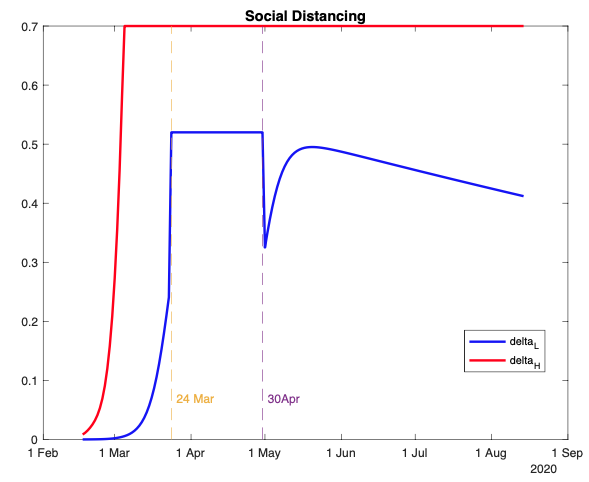
- Lifting these lockdown policies will eventually be followed by a second wave as low-risk individuals will respond to the flattening of the curve and the reduction of the mean contact rate during the intervention period by reducing their social distancing as soon as the lockdown is lifted (see Figure 7).
Figure 7
Notes: Equilibrium social distancing under no intervention (blue line) and an intervention (red line) that raises minimal social distancing from 0 to 0.52 for the period 24/03-30/04/2020. Otherwise, the underlying model is as in Figure 2.
- Raising the duration of such a lockdown would have a larger ‘flattening the curve’ effect but also a larger response by low-risk individuals.
- Instead, policies that raise the maximal level of social distancing (e.g. shutting down one third of essential sectors) lead to a significant drop in the death toll but do not have much impact on the evolution of the pool of infectious and the pool of susceptible people. In our simulations, such lockdown interventions that last between 5 and 8 weeks have almost identical effects on the pools of infectious and susceptible individuals. However, the longer the intervention period, the higher the negative effect on the death toll. The reason is that the behaviour of low-risk individuals stays largely unaffected, whereas high-risk individuals already exercise the maximal degree of social distancing before the start of the lockdown period and maintain maximal social distancing well beyond the end of an 8-week lockdown period.
- Interestingly, our calibrated model of the current UK epidemic suggests also that there might only be a small after-wave after lifting the simulated lockdown policy that raises the maximal level of social distancing. The reason is that, as we have mentioned above, whether there is a second wave or not depends also on the mean contact rate. The latter is endogenous in our model and according to the simulated lockdown policy above it is around 0.52 at the end of a 5-week intervention period. With a basic reproduction number of 2.25,9 this implies that there will be no second wave when the simulated lockdowns are lifted, if the proportion in the population that is still susceptible is at most equal to around 86%. This implies a much lower level of ‘herd immunity’ than is normally thought to be sufficient for the prevention of a second wave. In our calibrated model, the equilibrium proportion of susceptible people at the instant the simulated lockdown is lifted is around 92%, and so the effective reproduction number is only 1.076 (= 0.52 x 2.25 x 0.92).
Bearing in mind that, according to various news reports, most governments are not able the implement a complete lockdown, there will always be a margin for individuals to choose the extent of their self-isolation. As a result, even in the presence of lockdown interventions, low-risk individuals may still be exposed and get infected, generating herd immunity, while high-risk groups self-isolate to the maximum degree possible to minimise their risk of dying. This behaviour during partial lockdowns might be enough to bring the effective reproduction number very close to one and ensure that the after-wave is not big. Ultimately, whether this will be the case or not is a matter of quantitative analysis.
The quantitative predictions of the deployed model may change if the existing estimates we use are revised or if some of the underlying assumptions are no longer valid. This emphasises the need for more accurate estimates and further simulations of possible lockdown episodes by epidemiologists and the scientific community at large. However, our analysis highlights the importance of incorporating an economic analysis of social distancing in the typical epidemiological model for informing, and potentially modifying, existing arguments behind lockdown policies.
References
Baldwin, R and B Weder di Mauro (2020), Economics in the Time of COVID-19, a VoxEU.org eBook, CEPR Press.
Farboodi, M, G Jarosch and R Shimer (2020), “Internal and External Effects of Social Distancing in a Pandemic”, Becker Friedman Institute, Working Paper No 2020-47.
Galeotti, A, P Surico and J Steiner (2020), “The Value of Testing”, VoxEU.org, 23 April.
Kucharski, A J, T W Russell, C Diamond, Y Liu, J Edmunds, S Funk and R M Eggo (2020), “Early dynamics of transmission and control of COVID-19: a mathematical modelling study”, Lancet Infect Dis. 2020. doi: 10.1016/S1473-3099(20)30144-4.
Lourenço, J, R Paton, M Ghafari, M Kraemer, C Thompson, P Simmonds, P Klenerman and SS Gupta (2020), “ Fundamental principles of epidemic spread highlight the immediate need for large-scale serological surveys to assess the stage of the SARS-CoV-2 epidemic”, medRxiv.
Makris, M (2020), “Covid and Social Distancing with a Heterogenous Population”, University of Kent, Department of Economics Working paper Series No: 2002.
Toxvaerd, F (2020), “Equilibrium Social Distancing”, Cambridge-INET Working Paper Series No: 2020/08.
Wu, D, T Wu, Q Liu and Z Yang, (2020), “The SARS-CoV-2 outbreak: What we know”, International Journal of Infectious Diseases 94: 44–48.
Endnotes
1 For examples of other demonstrations of how economics can contribute in the management of the Covid-19 crisis, see Baldwin and Weder di Mauro (2020) and Galeotti at al. (2020).
2 One could, for instance, introduce more heterogeneity by allowing some of the low-risk individuals to die because of the infection but at a lower rate than that faced by the high-risk individuals. We could also add an incubation period, when people are infected but not infectious, a period of asymptomatic infectiousness, the potential of a discovery of a vaccine or a treatment or testing etc. These would increase further the predictive power of the SIR model, but the main insights of our discussion surrounding social distancing would still be relevant.
3 This model has been used, for instance, in Lourenço et. al. (2020), a study which found itself under the public spotlight in UK.
4 The paper will be updated here as revisions take place.
5 Adding an altruistic motive would make the infectious individuals to exercise social distancing as well, and the susceptible individuals to exercise higher social distancing if it is feasible. This would only strengthen the downward effects of endogenous social distancing on the mean contact rate and thereby the impact of social distancing on the evolution of the epidemic and death toll.
6 The same data, and for the same reason, were also used in Lourenço et. al. (2020).
7 Toxvaerd (2020) and Farboodi (2020) also study an SIR model with endogenous social distancing. However, both assumes a homogenous population, and Toxvaerd (2020) does not calibrate his model.
8 In Lourenço et al. (2020) the corresponding number is 0.08%.
9 Kucharski et. al. (2020) report a median estimate of R0 = 2.35 and Wu et. al. (2020) report an estimate of R0 = 2.2.