The famous Keynesian beauty contest literature emphasises the strategic complementarity in forecasting the forecasts of others. Keynes (1936) suggested that such a mechanism could be at work in stock markets, with share prices determined not just by fundamentals but also according to how investors think that other investors value particular shares. We believe that a beauty contest mechanism may operate in bond markets too, in which case the term structure of interest rates depends not only on the compensation an investor demands for holding bonds of different maturities, but also on what compensation the investor thinks that other investors will demand for holding the bonds.
The six winners in the beauty contest of the Sunday Times. The Washington Times, 5 May 1907. National Digital Newspaper Program, Library of Congress.
We are far from the first to write about the drivers of term structure. A search for journal articles with the phrase “term structure of interest rates” in the title gives 879 hits in EconLit and 186 hits in JSTOR. Despite this voluminous literature, quantitative macroeconomic models of the type developed by Christiano et al. (2005) and Smets and Wouters (2003, 2007) still struggle to generate risk premia anything like those seen in financial markets. For example, Rudebusch and Swanson (2012) find an average term premium of about one basis point on nominal 10-year bonds in a medium-scale dynamic stochastic general equilibrium (DSGE) model with nominal rigidities and a reasonable coefficient of relative risk aversion. Estimates from Adrian et al. (2013) suggest that the term premium on 10-year US Treasuries between 1999 and 2017 was two orders of magnitude higher at over 100 basis points.
Rudebusch and Swanson (2008) refer to the disconnect between financial market data and models of the term structure as the bond premium puzzle, to mirror the well-known equity premium puzzleof Mehra and Prescott (1985). Mechanisms proposed to explain the latter include recursive preferences (Epstein and Zin 1989), long-run risk (Bansal and Yaron 2004), rare disasters (Barro 2006) and habit formation (Abel 1999). However, models which include one or more of the above mechanisms typically explain data on risk premia only at the expense of implausibility remaining at some other margin. This continues to be the case when these mechanisms are used to explain the bond premium puzzle. Rudebusch and Swanson (2012) ask whether a medium-scale DSGE model with recursive preferences and a plausible degree of long-term risk can match the term premium on a nominal 10-year bond. The answer is yes, but only in a specification where the coefficient of relative risk aversion is 110.
The bond premium puzzle arises because the excess yield that investors require to hold a long-term bond is too small in quantitative macroeconomic models. In a new paper, we present a new decomposition that stresses the importance of informational frictions for the emergence of sizeable term premia (Ellison and Tischbirek 2018). By applying the law of total covariance to the standard no-arbitrage pricing condition, the average term premium at any given maturity is shown to depend on the covariances of successive realisedstochastic discount factors and the covariances of successive expectationsof stochastic discount factors, with the latter being directly affected by the informational assumptions imposed on the model. The new decomposition prompts us to attribute the quantitative failure of medium-scale DSGE models to the imposition of information assumptions that do not deliver sufficient covariance in expectations.
If there is full information in a simple analytical model, then we find that the expectations of investors are well-anchored to fundamentals so both the expectations component of the term premium and the term premium itself are small. Little changes if investors have to work out whether shocks are transitory or permanent. The signal extraction problem under such partial information induces some extra covariance in successive expectations, but nowhere near enough to generate significant term premia. If information is noisy then term premia actually fall, as the covariance in successive expectations is dampened rather than magnified by signal extraction.
The inability of either partial or noisy information to support meaningful term premia suggests a need for more radical informational assumptions. Shiller (1984) offers some guidance:
“Since investors lack any sense of objective evidence regarding prices of speculative assets, the process by which their opinions are derived may be especially social”.
The idea that social processes might drive investor opinion motivates us to introduce strategic complementarities in the formation of expectations. Doing so also draws on work changing the informational assumptions in macroeconomic models to explain the behaviour of selected financial assets, most notably the beauty contest literature of Morris and Shin (2002) and the finding that strategic motives can amplify volatility in aggregate expectations in Angeletos and La’O (2013).
We introduce a strategic complementarity in the formation of expectations by giving investors an incentive to make forecasts of their stochastic discount factor that are in line with the forecasts made by other investors, a ‘forecasting the forecasts of others’ problem. When coupled with the assumption that information is both private and public, this proves to be a powerful mechanism that generates substantial covariance in successive expectations of stochastic discount factors and hence sizeable term premia.
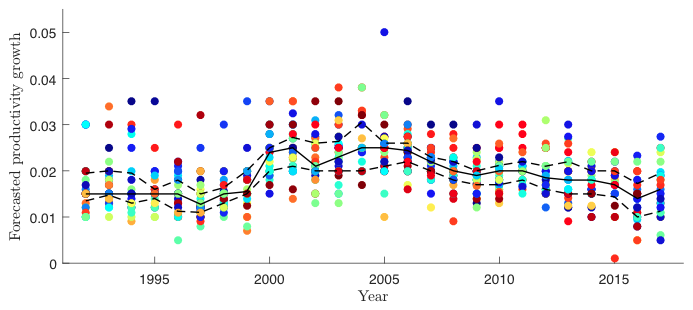
In confronting our model with US data, we ask whether a quantitative model with realistic levels of strategic complementarities can explain average term premia without resorting to excessive levels of risk aversion. To discipline our estimations, we require that the one-year term premium in the model matches the estimate in US data from Adrian et al. (2013) and that the degree of strategic complementarities in forecasting is consistent with the cross-sectional and time series properties of productivity growth forecasts from the Survey of Professional Forecasters in Figure 1.
Figure 1 Forecasts of productivity growth from the Survey of Professional Forecasters
Each dot of the same colour in Figure 1 represents an individual forecaster’s year-by-year view of expected productivity growth over the following ten years. The solid line is the median and the dashed lines are the upper and lower quartiles. The properties of the forecasts in Figure 1 are relevant because expected technology growth is key when investors forecast their stochastic discount factors. Requiring the properties of forecasts made in the model to match those in the Survey of Professional Forecasters imposes tight discipline on our estimation.
We find a role for strategic complementarities in explaining the forecasts from the Survey of Professional Forecasters, by estimating that investors place a positive weight on their forecasts having the same sign as the expected average forecast of other investors. The model is able to match the average term premium on a one-year Treasury with a reasonable coefficient of relative risk aversion of 4.6.
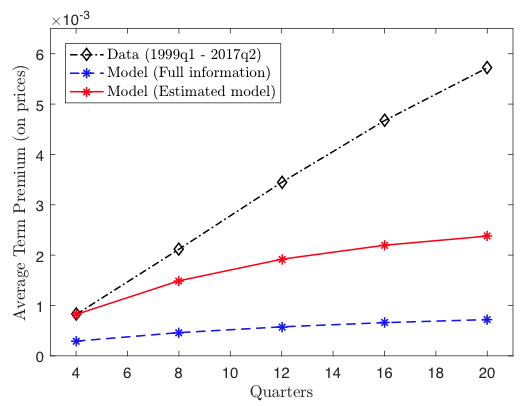
Figure 2 Term premia in the data and in the models
The ultimate test of the model is its ability to generate significant term premia. The model delivers annualised real-term premiums of 14.9, 19.2, 22.0 and 23.8 basis points at two-, three-, four- and five-year horizons, between 40% and 70% of the corresponding annualised nominal term premia in the data. Our findings stress the importance of information assumptions in models of the term structure of interest rates, as is starkly visible in Figure 2 when comparing the red line for the term structure in our model with a beauty contest to the black line for that in the data. The estimated model exactly matches the term premium at the short end since it is targeted in estimation, but in doing so the data prefers strategic complementarities over an unrealistically high coefficient of relative risk aversion. With these strategic complementarities in place, the estimated model explains a significant proportion of the term premium at all maturities, even though they have not been targeted in estimation. The full information model in blue is singularly unable to do this with realistic levels of risk aversion, failing to deliver either term premia that are sizeable or a term structure that is upward-sloping.
References
Abel, A B (1999), “Risk premia and term premia in general equilibrium”, Journal of Monetary Economics 43(1): 3-33.
Adrian, T, R K Crump and E Moench (2013), “Pricing the term structure with linear regressions”, Journal of Financial Economics 110(1): 110-138.
Angeletos, G and J La’O (2013), “Efficient use of information and social value of information”, Eocnometrica 75(4): 1103-1142.
Bansal, R and A Yaron (2004), “Risks for the long run: A potential resolution of asset pricing puzzles”, Journal of Finance 59(4): 1481-1509.
Barro, R J (2006), “Rare disasters and asset markets in the twentieth century”, Quarterly Journal of Economics 121(3): 823-866.
Christiano, L J, M Eichenbaum and C L Evans (2005), “Nominal rigidities and the dynamic effects of a shock to monetary policy”, Journal of Political Economy 113(1): 1-45.
Ellison, M and A Tischbirek (2018), “Beauty contests and the term structure”, CEPR Discussion Paper No. 12762.
Epstein, L G and S E Zin (1989), “Substitution, risk aversion, and the temporal behaviour of consumption and asset returns: A theoretical framework”, Econometrica 57(4): 937-969.
Keynes, J M (1936), The general theory of employment, interest and money, Basingstoke: Palgrave Macmillan.
Mehra, R and E C Prescott (1985), “The equity premium: A puzzle”, Journal of Monetary Economics 15(2): 145-161.
Morris, S and H S Shin (2002), “Social value of public information”, American Economic Review 92(5): 1521-1534.
Rudebusch, G D and E T Swanson (2008), “Examining the bond premium puzzle with a DSGE model”, Journal of Monetary Economics 55: S111-S126.
Rudebusch, G D and E T Swanson (2012), “The bond premium in a DSGE model with long-run real and nominal risks”, American Economic Journal: Macroeconomics 4(1): 105-143.
Shiller, R J (1984), “Stock prices and social dynamics”, Brookings Papers on Economic Activity 2: 457-498.
Smets, F and R Wouters (2003), “An estimated dynamic stochastic general equilibrium model of the Euro area”, Journal of the European Economic Association 1(5): 1123-1175.
Smets, F and R Wouters (2007), “Shocks and frictions in US business cycles: A Bayesian DSGE approach”, American Economic Review 97(3): 586-606.