Whether the equity premium is predictable has been the subject of long debate in finance. While a large literature documents in-sample predictability (e.g. Fama and French 1988, Lettau and Ludvigson 2001), the evidence in favour of robust out-of-sample stock return predictability has been mixed. In an influential study, Welch and Goyal (2008) argued that many of the suggested predictors would not have helped an investor to time the market in real time, and that popular predictor variables often only ‘worked’ during certain periods of time. In the meantime, a growing body of literature has proposed alternative stock return predictor variables. A common pattern that emerges from this literature is that stock returns appear to be predictable mainly around recessions.
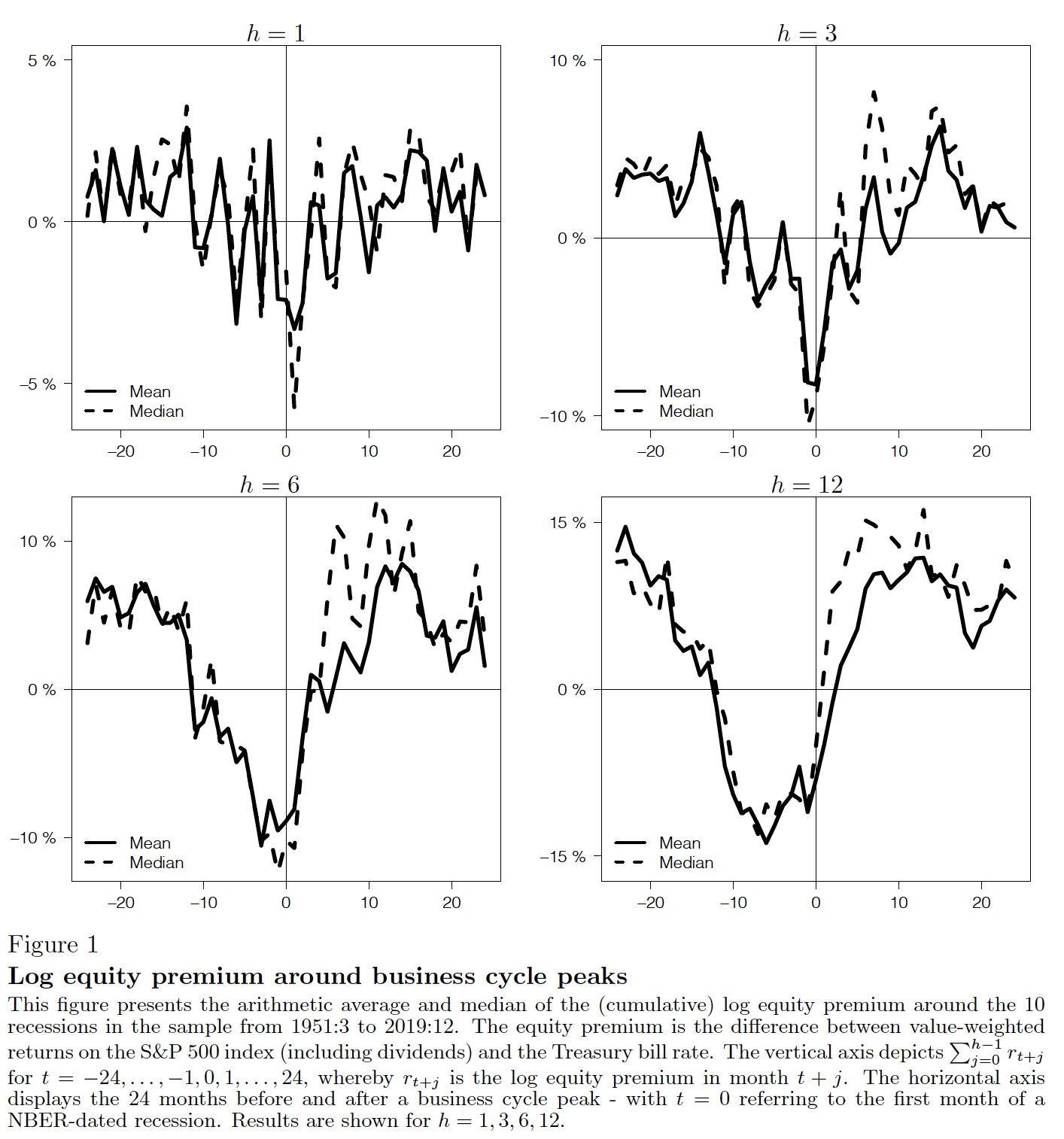
In a recent paper (Moench and Stein 2021), we expand on this literature and document that the monthly US equity premium is strongly predictable based on information that signals recessions. Figure 1 plots the forward-looking mean and median of the log US equity premium over different time windows around the ten US recessions from 1951 through 2019. Stock returns follow a striking ‘V-shaped’ pattern, with sharply negative returns heading into recessions and a strong recovery as the recession unfolds. Excess stock returns are on average sharply negative in the one- to two-year window around the peak and large and positive thereafter. Indeed, when excluding two years of observations around each peak, the equity premium increases to 11.1% from 6.3% for the full sample, and the annual Sharpe ratio doubles from 0.4 to 0.8.
Figure 1 Log equity premium around business cycle peaks
Predicting recessions with the term spread
It is well documented that US recessions in the post-war period have all been preceded by an inverted Treasury yield curve. This means that the term spread, the difference between yields on long-term and short-term Treasury securities, typically drops into negative territory before recessions start. A large literature going back to Estrella and Hardouvelis (1991) has therefore predicted US recessions using the term spread. Recent work (Liu and Moench 2016) has documented that information about the prior path of the term spread – over and above its current level – further improves recession forecasts.
In our analysis, we combine the insights from the recession prediction literature with our initial observation that stock returns have a strong V-shaped pattern around business cycle peaks. Precisely, we show that model-implied recession probabilities based on information in the yield curve significantly predict the equity premium out-of-sample and help to profitably time the market.
To predict recessions as defined by the Business Cycle Dating Committee of the National Bureau of Economic Research (NBER), we estimate several probit model specifications that make use of information in the term spread in different ways. The first model is in the spirit of Estrella and Hardouvelis (1991) and only includes the term spread (TMS) and a constant as predictors. The second model includes a six-month lagged term spread following Liu and Moench (2016), and the third includes a three-year backward-looking moving average of the term spread (MA-TMS) as additional predictors.
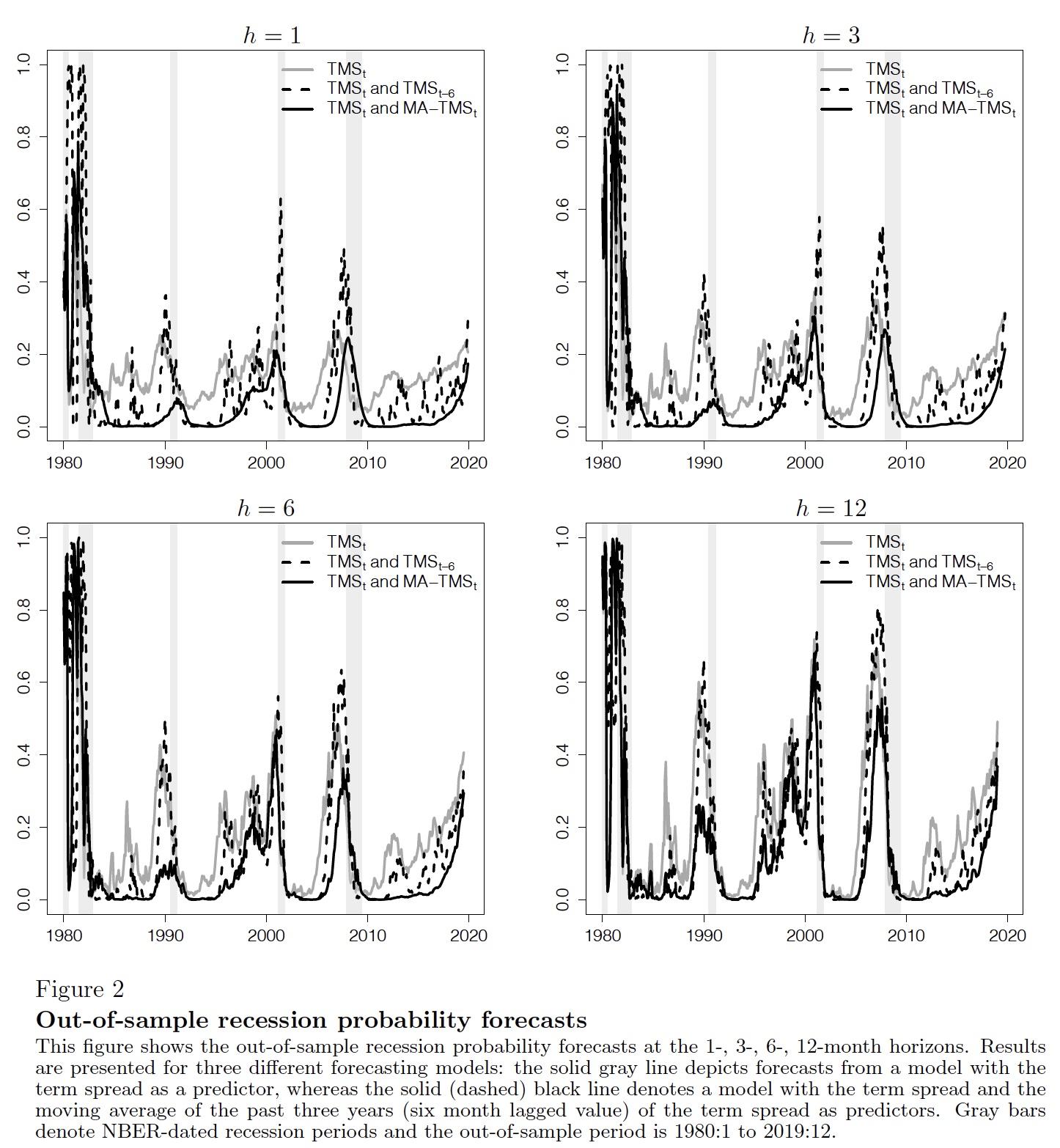
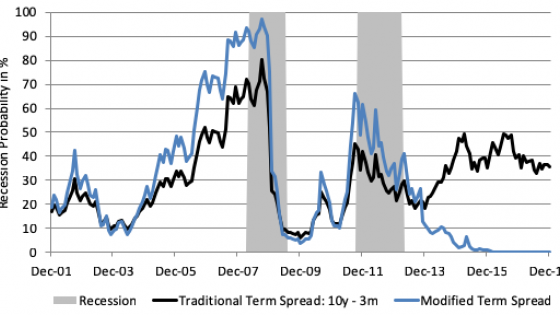
Figure 2 shows the out-of-sample recession probability forecasts for the three probit models from January 1980 to December 2019. Consistent with the prior literature, the model with only the term spread and a constant performs poorly for horizons of less than a year and generates a number of false positive signals of recessions. The models with lagged term spread (TMS) and moving-average term spread (MA-TMS) perform substantially better for short-horizon forecasts. In addition, the estimates derived by the model including the term spread and the moving average term spread imply smooth recession probabilities. All three models have in common that the implied recession probabilities since the mid-1980s are relatively muted and rarely exceed 50%. This observation is consistent with prior research finding evidence for a structural break in the probit model (e.g. Chauvet and Potter 2002, Galvão 2006).
Figure 2 Out-of-sample recession probability forecasts
Adjusting for a structural break in the mean of the term spread
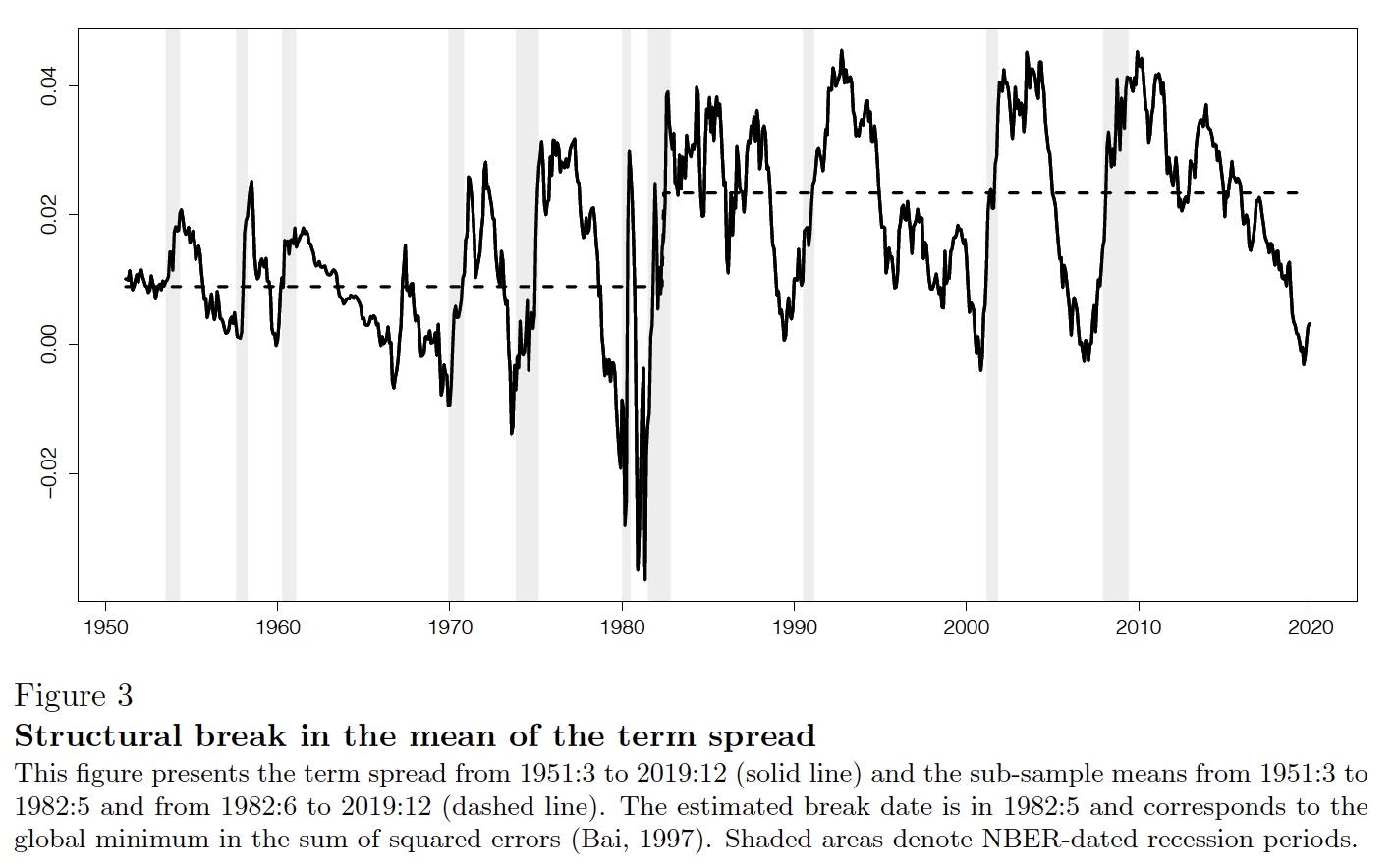
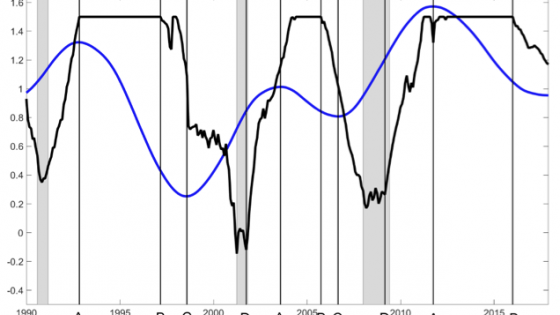
Applying commonly used break tests (Andrews and Ploberger 1994), we indeed document a structural break in the mean of the term spread in 1982. We show that this break could have been identified by investors as early as 1986. Figure 3 plots the term spread and the estimated sub-sample means for the periods before and after the break.
Figure 3 Structural break in the mean of the term spread
We follow Pesaran and Timmermann (2007) and Lettau and Van Nieuwerburgh (2008) and implement several approaches to correct for this break in real-time. All significantly improve the predictability of recessions out-of-sample. Not surprisingly, this improvement is driven by the fact that the recession probabilities are less muted after the structural break in 1982.
Predicting the equity premium with recession probabilities
The model-implied recession probabilities typically rise ahead of recessions and then fall back to zero during or after the recession. As such they are the mirror image of the V-shaped pattern of equity returns that we have documented above. We therefore use these probabilities as inputs in a simple linear regression model to predict the equity premium over horizons from one month to one year out. We make sure not to use any information that would not have been available to investors in real-time. Specifically, as the classification into recessions and expansions by the NBER is not available in real time, we account for a publication delay of two years to rule out any look-ahead bias. We use mean squared forecast errors as the evaluation criterion and compare our forecasts to a simple – yet difficult to beat – benchmark that forecasts a constant equity premium (Welch and Goyal 2008).
We find that the models based on the lagged term spread and moving average term spread consistently outperform this benchmark over forecast horizons of 1, 3, 6, and 12 months. Adjusting for the break in the term spread further improves the model predictions. Importantly, recession probabilities outperform the historical average benchmark not just in recessions but also in expansions. The reason is that by correctly anticipating low equity market returns heading into recessions, they also correctly predict higher returns in business cycle booms. We also show in the paper that the break-adjusted recession probabilities outperform other recently proposed predictors.
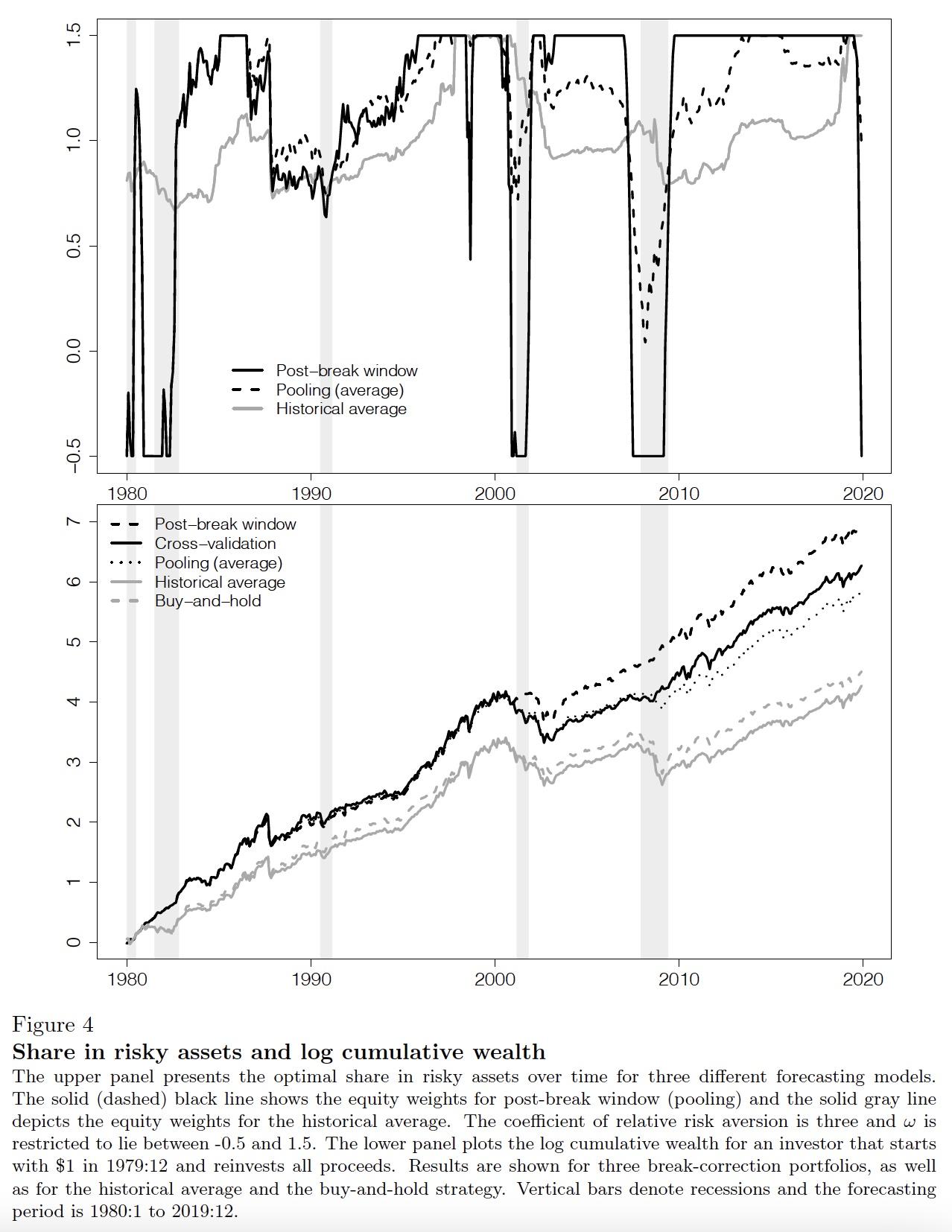
We evaluate the economic relevance of our forecasts with a simple investment strategy where an investor can allocate funds between the stock market and the risk-free rate. The weights are restricted to lie between -0.5 and 1.5 (leveraging and short selling up to 50%). The upper panel in Figure 4 presents the share in risky assets based on two different break-adjusted recession probabilities as well as for the historical average. While weights for the latter forecasts move only slowly, the two recession probability based return forecasts imply strong portfolio rebalancing around recessions. The equity market exposure is reduced prior to the start of recessions when the yield curve flattens and then quickly reversed when the yield curve steepens again. During expansions the equity share is higher compared to the historical average and the buy-and-hold strategy.
Figure 4 Share in risky assets and log cumulative wealth
The lower panel in Figure 4 shows the log cumulative wealth of an investor who would have started with $1 in December 1979 and would have reinvested all proceeds according to the different models. While the historical average and the buy-and-hold strategy perform relatively poor in recessions – with severe losses particularly in the global crisis of 2008-09 – the recession probability-based models give rise to higher and less volatile profits over time. In our paper we show that these results extend to portfolio sorts based on different characteristics and to other countries and are robust to several modelling choices. We conclude that information in the yield curve can be used to time the equity market.
References
Andrews, D W K and W Ploberger (1994), “Optimal Tests when a Nuisance Parameter is Present Only Under the Alternative”, Econometrica 62: 1383-1414.
Bai, J (1997), “Estimation of a change point in multiple regression models”, Review of Economics and Statistics 79: 551-563.
Chauvet, N and S Potter (2002), “Predicting a recession: evidence from the yield curve in the presence of structural breaks”, Economics Letters 77: 245-253.
Estrella, A and G A Hardouvelis (1991), “The Term Structure as a Predictor of Real Economic Activity”, Journal of Finance 46: 555-576.
Fama, E F and K R French (1988), “Dividend yields and expected stock returns”, Journal of Financial Economics 22: 3-25.
Galvão, A B (2006), “Structural Break Threshold VARs for Predicting US Recessions using the Spread”, Journal of Applied Econometrics 21: 463-487.
Lettau, M and S Ludvigson (2001), “Consumption, Aggregate Wealth, and Expected Stock Returns”, Journal of Finance 56: 815-849.
Lettau, M and S Van Nieuwerburgh (2008), “Reconciling the Return Predictability Evidence”, Review of Financial Studies 21: 1607-1652.
Liu, W and E Moench (2016), “What predicts US recessions?”, International Journal of Forecasting 32: 1138-1150.
Moench, E and T Stein (2021), “Equity premium predictability over the business cycle”, CEPR Discussion Paper No. 16357.
Pesaran, M H and A Timmermann (2007), “Selection of estimation window in the presence of breaks”, Journal of Econometrics 137: 134-161.
Welch, I and A Goyal (2008), “A Comprehensive Look at The Empirical Performance of Equity Premium Prediction”, Review of Financial Studies 21: 1455-1508.