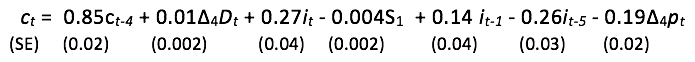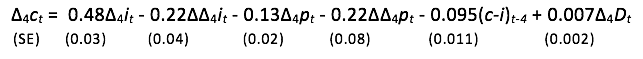There are two main approaches to empirically modelling a relationship: theory driven and data driven. In the former, common in economics, the putative relation is derived from a theoretical analysis claimed to represent the relevant situation, then its parameters are estimated by imposing that `theory model’ on the data. When the variable to be modelled is denoted yt, the set of n explanatory variables is zt, and the theory relation is yt = f(zt), then the parameters of f(.) are estimated from a sample of data over t = 1,…,T. In what follows, we use a simple aggregated `permanent income’ (PIH) consumption function as our example (see, for example, Ball et al. 1975) for log(consumption), c, log(income), i, and lagged c. When yt = f(zt) + et in reality, where et is a small, independent, identically distributed perturbation, directly estimating the theory model is essentially optimal, but is obviously less useful when the postulated relationship is either incomplete (in that excluded variables such as inflation, shifts and other lags also influence yt, as in Davidson et al. 1978, denoted DHSY), incorrect (in that the assumed f(.) is not the actual function relating c to i and lagged c) or f(.) changes over the sample, due to (say) financial liberalisation, etc (e.g. Duca and Muellbauer 2013).
In a data-driven approach, observations on a larger set of N > n variables {xt} are collected to `explain’ yt, which here could augment disposable income with interest rates, inflation, taxes, unemployment, wealth, the relative price of durables to non-durables, etc. Their choice is based on looser theoretical guidelines, then some method of model selection is applied to pick the `best’ relation between yt and a subset of the xt within a class of functional connections (such as a linear relation with constant parameters and small, identically-distributed errors independent of the xt). When N is very large (`big data’, which could include micro-level data on household characteristics or internet search data), most current approaches have difficulties either in controlling the number of spurious relationships that might be found (because of an actual or implicit significance level for hypothesis tests that is too loose for the magnitude of 2N), or in retaining all of the relevant explanatory variables with a high probability (because the significance level is too stringent) (e.g. Doornik and Hendry 2015). Moreover, the selected model may be hard to interpret, and if many equations have been tried (but perhaps not reported), the statistical properties of the resulting selected model are unclear (see Leamer 1983).
The drawbacks of using theory-driven or data-driven approaches in isolation
Many variants of theory-driven and data-driven approaches exist, often combined with testing the properties of the {et}, the assumptions about the regressors, and the constancy of the relationship f(.), but with different strategies for how to proceed following rejections of any of the conditions required for viable inference. The assumption made all too often is that rejection occurs because the test has power under the specific alternative for which the test is derived, although a given test can reject for many other reasons. The classic example of such a `recipe’ is finding residual autocorrelation and assuming it arose from error autocorrelation, whereas the problem could be mis-specified dynamics, unmodelled location shifts, or omitted autocorrelated variables. In the consumption function example, in order to eliminate autocorrelation, seasonal and annual dynamics need to be modelled, along with shifts due to tax and other legislative changes. The approach proposed in the next section instead seeks to include all likely determinants from the outset, and would revise the initial general formulation if any of the mis-specification tests thereof rejected.
Most observational data are affected by many influences, often outside the relevant subject’s purview – as 2016 emphasised for economics – and it would require a brilliant theoretical analysis to take all the substantively important forces into account. Thus, a purely theory-driven approach, such as a solved-out theory-consistent aggregate consumption function, is unlikely to deliver a complete, correct, and immutable model that forges a new `law’ once estimated. Rather, to capture the complexities of real world data, features outside the theory remit almost always need to be taken into account, especially changes resulting from unpredicted events. Few theories include all the variables that characterise a process, with correct dynamic reactions, and the actual non-linear connections. Moreover, the data may be mis-measured for the theory variables (such as revisions of national accounts data for different vintages), and may even be incorrectly recorded relative to its own definition, leading to outliers. Finally, shifts in relationships are all too common – there is a distinct lack of empirical models that have stood the test of time or have an unblemished forecasting track record (Hendry and Pretis 2016).
Many of the same problems affect a purely data-driven approach unless the {xt} provide a remarkably comprehensive specification, in which case there will often be more candidate variables N than observations T (see Castle and Hendry 2014 for a discussion of that setting). Because included regressors will `pick up’ influences from any correlated missing variables, omitting important factors usually entails biased parameter estimates, badly behaved residuals, and often non-constant models. Consequently, failing to retain any of the relevant theory-based variables can be pernicious and potentially distort which models are selected. Thus, an approach that retains, but does not impose, the theory-driven variables without affecting the estimates of a correct, complete, and constant theory model, yet also allows selection over a much larger set of candidate variables to avoid the substantial costs that result if relevant variables are missing in the initial specification, has much to offer. We now describe how the benefits of the two approaches can be combined to achieve that outcome based on Hendry and Doornik (2014) and Hendry and Johansen (2015).
A combined approach
Assume the theory correctly specifies the set zt of n relevant variables entering f(.), then to explain our approach, for simplicity we use the explicit parametrisation for f(.) of a linear, constant parameter vector β, so the theory model is yt = β’zt + et where et is an independent identically distributed Normal random variable, independent of zt. This formulation could represent an equilibrium-correction formulation, and is the relation to be retained while selecting over an additional set of M candidate variables denoted {wt}. These could include disaggregates for household characteristics (in panel data), as well as the variables noted above. To ensure an encompassing explanation, wt might include lags and non-linear functions of the {zt} and other explanatory variables used by different investigators, as well as indicator variables to capture potential outliers and shifts. Then, formulate the general unrestricted model (GUM) as:
yt = β'zt + γ'wt + vt
which nests both the theory model and the data-driven formulation when xt = (zt, wt), so vt will inherit the properties of et when γ = 0. Even so, under the correct theory specification, because zt and wt are usually quite highly correlated, estimation of the GUM will rarely deliver the same estimates of β as direct estimation of the theory model.
The key step in the approach here is that without loss of generality, zt can be orthogonalised with respect to wt by projecting the latter onto the former in:
wt = Γzt + ut
where E[ztut'] = 0 for estimated Γ. Substitute the estimated components Γzt and ut for wt in the GUM, leading to:
yt = β'zt + γ'(Γzt + ut) + vt = (β' + γ'Γ)zt + γ’ut + vt
When γ = 0, the coefficient of zt remains β, and because zt and ut are now orthogonal by construction, the estimate of β is unaffected by whether or not any or all ut are included. Thus, data-based model selection can be applied to all the potential additional candidate explanatory variables while retaining the theory model without selection.
Such selection can be undertaken at a stringent significance level, say α = min(0.001,1/N) to minimize the chances of spuriously selecting irrelevant ut, yet protecting against missing important explanatory variables, such as location shifts. The critical value for 0.1% in a Normal distribution is c0.001 ≈ 3.35, so substantive regressors or shifts should still be easily retained. As noted in Castle et al. (2011), using impulse-indicator saturation (IIS) allows near Normality to be a reasonable approximation (see Johansen and Nielsen 2009, 2016 for formal analyses of the properties of IIS). However, a reduction from an integrated to a non-integrated representation requires non-Normal critical values, another reason for using tight significance levels during model selection.
When should an investigator reject the theory specification yt = β'zt + vt? As there are M variables in wt, on average αM will be significant by chance, so if M = 100 and α = 1% (so c0.01 ≈ 2.6), on average there will be one adventitiously significant selection. Thus, finding that one of the ut was `significant’ would not be surprising even when the theory model was correct and complete. Indeed, the probabilities that none, one and two of the ut are significant by chance are 0.37, 0.37 and 0.18, leaving a probability of 0.08 of more than two being retained. However, using α = 0.5% (c0.005 ≈ 2.85), these probabilities become 0.61, 0.30 and 0.08 with almost no probability of 3 or more being significant; and 0.90, 0.09 and <0.01 for α = 0.1%, in which case retaining 2 or more of the ut almost always implies an incomplete or incorrect theory model.
When M + n = N > T, our approach can still be implemented by splitting the variables into feasible sub-blocks wi,t, estimating separate projections for each sub-block, and replacing these subsets wi,t by their residuals ui,t. The n variables wt are retained without selection at every stage, only selecting over the (hopefully irrelevant) variables ui,t at a stringent significance level using a multi-path block search of the form implemented in the model selection algorithm Autometrics (Doornik 2009, Doornik and Hendry 2013). When the initial theory model is incomplete or incorrect – a likely possibility for the consumption function illustration here – but some of the wt are relevant to explaining yt, then an improved empirical model should result.
An illustration of the combined approach using the original DHSY data set
Starting from the simplest version of the PIH, ct = β0 + β1it + β2ct-1 + et, on quarterly UK data, with added seasonal dummies (Si), could DHSY have found their model in an afternoon rather than several years? Estimates of the PIH equation over 1958(2) - 1976(2) yielded:
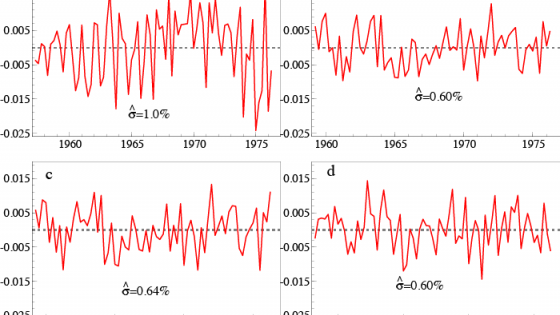
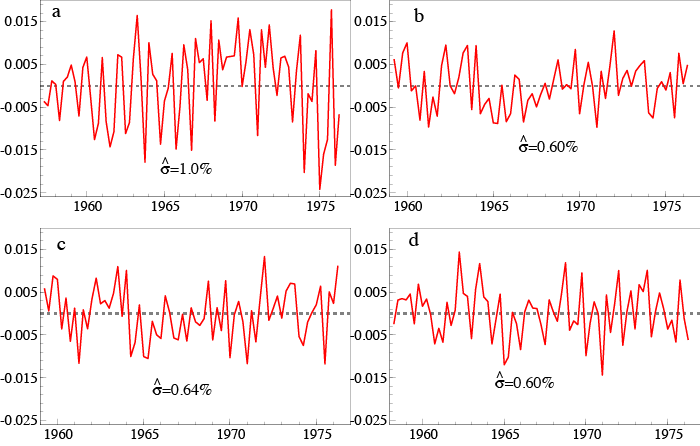
where σ = 1.0%, but tests for residual autocorrelation, ARCH and heteroskedasticity all reject (see Figure 1a for a graph of the resulting residuals). A glance at the data on ct suggests that seasonal lags might matter (here five lags), and including the inflation variables (Δ4p) and tax dummy (Δ4Dt) from DHSY delivers the GUM. We orthogonalised all these variables as above and estimated the GUM to check that the coefficient estimates of the PIH retained variables were unaffected. We then selected from the additional variables at α = 1%. Given the small sample size (73) and M=12, a significance level of 1% means that on average only one variable will be selected by chance every eight times such a model is selected from. The orthogonal components for ct-4, it-1, it-5, and Δ4pt were selected, with a joint significance of F(4,58)= 31.3 which strongly rejects their irrelevance at any sensible significance level (see Figure 1b for a graph of the residuals). Replacing the orthogonalised variables by the original to formulate the original GUM above given the theory rejection, and selecting over all the candidates, including the theory variables, yielded:
with σ = 0.64%, where no mis-specification tests rejected (see Figure 1c) (estimation of the levels formulation is justified by Sims et al. 1990). The approach enables us to take seriously the PIH theory, but also allow for many other effects that lie outside the confines of the theory.
A reduction to a non-integrated representation can be applied by selecting from the initial GUM in the original measures after transforming to seasonal differences and differentials, and when no variables were retained without selection, this yielded:
with σ = 0.60%, and again no mis-specification tests rejected (see Figure 1d). This essentially recovers DHSY in a couple of hours – oh for having had the current technology in the 1970s! This is only partly anacrochonistic, as the theory in Hendry and Johansen (2015) could easily have been formulated 50 years ago. Combining the theory and data based approaches has resulted in a well-specified, theory interpretable model.
Figure 1
Conclusions
In our proposed combined theory-driven and data-driven approach, when the theory is complete it is almost costless in statistical terms to check the relevance of large numbers of other candidate variables, yet there is a good chance of discovering a better empirical model when the theory is incomplete or incorrect. Automatic model selection algorithms that allow retention of theory variables while selecting over many orthogonalised candidate variables can therefore deliver high power for the most likely explanatory variables while controlling spurious significance at a low level.
References
Ball, R J, D B Boatwright, T Burns, P W M Lobban and G W and Miller (1975), “The London Business School Quarterly Econometric Model of the U.K. Economy”, in G A Renton (ed), Modelling the Economy, London: Heinemann Educational Books, pp. 3–37
Castle, J L, J A Doornik and D F Hendry (2011), “Evaluating automatic model selection”, Journal of Time Series Econometrics 3 (1), DOI: 10.2202/1941–1928.1097.
Castle, J L, J A Doornik and D F Hendry (2012), “Model selection when there are multiple breaks”, Journal of Econometrics, 169, 239–246.
Castle, J L and D F Hendry (2014), “Semi-automatic non-linear model selection”, Ch. 7 in N Haldrup, M Meit and P and Saikkonen (eds), Essays in Nonlinear Time Series Econometrics. Oxford: Oxford University Press.
Castle, J L and N Shephard (eds) (2009), The Methodology and Practice of Econometrics. Oxford: Oxford University Press.
Davidson, J E H, D F Hendry, F Srba and J S and Yeo (1978), “Econometric Modelling of the Aggregate Time-Series Relationship between Consumers' Expenditure and Income in the United Kingdom”, Economic Journal, 88, 661–692.
Doornik, J A (2009), “Autometrics”, in J L Castle and N Shephard (eds) (2009), The Methodology and Practice of Econometrics. Oxford: Oxford University Press, pp. 88–121.
Doornik, J A and D F Hendry (2013), Empirical Econometric Modelling using PcGive: Volume I, 7th edn. London: Timberlake Consultants Press.
Doornik, J A and D F Hendry (2015), “Statistical Model Selection with Big Data”, Cogent Economics and Finance.
Duca, J and J N J Muellbauer (2013), “Tobin LIVES: Integrating evolving credit market architecture into flow of funds based macro-models”, in B Winkler, A van Riet and P Bull (eds), A Flow of Funds Perspective on the Financial Crisis, Volume II, Palgrave Macmillan, pp. 11–39
Hendry, D F and J A Doornik(2014), Empirical Model Discovery and Theory Evaluation. Cambridge, MA: MIT Press.
Hendry, D F and S Johansen (2015), “Model discovery and Trygve Haavelmo’s legacy”, Econometric Theory, 31, 93–114.
Hendry, D F, S Johansen and C Santos (2008), “Automatic selection of indicators in a fully saturated regression”, Computational Statistics, 33, 317–335. Erratum, 337–339.
Hendry, D F and F Pretis (2016), “All Change! Non-stationarity and its implications for empirical modelling, forecasting and policy”, Oxford Martin School Policy Paper.
Johansen, S and B Nielsen (2009), “An analysis of the indicator saturation estimator as a robust regression estimator”, in in J L Castle and N Shephard (eds) (2009), The Methodology and Practice of Econometrics. Oxford: Oxford University Press, pp. 1–36.
Johansen, S and B Nielsen (2016), “Asymptotic Theory of Outlier Detection Algorithms for Linear Time Series Regression Models”, Scandinavian Journal of Statistics, 43, 321–348.
Leamer, E E (1983), “Let’s take the con out of econometrics”, American Economic Review, 73, 31–43.
Sims, C A, J H Stock M W and Watson (1990), “Inference in Linear Time Series Models with Some Unit Roots”, Econometrica, 58, 113–144