A group of the world’s leading mathematicians gathered at the College de France in Paris in June 2000, where the Clay Mathematics Institute (CMI) announced seven Millennium Prize Problems. The prizes – along with a million dollars for the solution of each problem – were conceived “to spread the news that in mathematics hard, significant problems still abound – the frontiers of knowledge are still wide open.”
In scientific fields there is an important open question about how to motivate future generations to engage in knowledge production and advance the knowledge frontier. Philanthropists and governments have tried to promote innovation through rewarding research outputs (‘pull’ incentives) or providing upfront support for research inputs (‘push’ programs) (Kremer and Williams 2010). A common pull incentive used to promote discoveries in science is the use of prizes, such as the Nobel Prize or the Millennium Prize (Maurer and Scotchmer 2004). There is also widespread use of push programmes to stimulate discoveries in science – such as grants that cover research costs in advance or fellowships for gifted students to pursue scientific careers (Stephan 2012, Williams 2012).
In practice, various combinations of pull and push incentives have been used simultaneously, but we are only starting to learn about the effectiveness of each tool in advancing the knowledge frontier. One notable instance of the knowledge frontier moving is the proof of the Poincare conjecture (one of the seven Millennium Problems) provided by the Russian mathematician Grigori Perelman in 2002. This was striking because the problem had eluded the best minds for over a century, and many mathematicians speculated that another century could pass before a solution was found (Overbye 2006). For his solution Perelman was awarded the Fields Medal in 2006 (the most prestigious award in mathematics), the Millennium Prize in 2010, and several tenured positions at the world’s top mathematics departments – all of which he declined. It appears that at least in this particular case, pull incentives were not explicitly at work (Overbye 2006). Instead, biographers suggested that it was his “mind of unrivalled computational power” honed from an early age in special Russian schools that enabled Perelman to solve the problem (Gessen 2009, Szpiro 2008). Indeed, Perelman had been recognised as an exceptional talent in his youth, and had achieved a perfect score at the 1982 International Mathematics Olympiad. Perelman’s success raises the question of whether exceptional youth talent could also be important for advancing the knowledge frontier more generally? And, if so, are there many other exceptional talents like Perelman out there that have been lost or are at-risk of being lost to the world of science?
New research is starting to shed light on these questions. In a new paper, we study knowledge production in mathematics and use a unique institutional feature of this discipline – the International Mathematics Olympiads (IMO), a prominent worldwide competition for high-school students (Agarwal and Gaule 2018). This setting allows us to measure talent in teenage years in a comparable way across multiple countries. We follow these participants over their lifetime and evaluate their lifetime knowledge production.
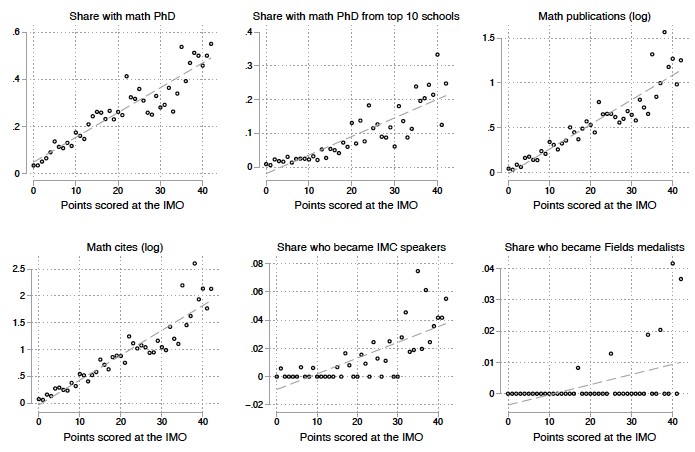
Figure 1 IMO results and outcomes
We find that even in this group of teenagers in the extreme right tail of the talent distribution, small differences in talent are associated with sizeable differences in long-term achievements, including getting a PhD, number of mathematics publications and cites, and being awarded a Fields medal. For instance, each additional point scored on the IMO by a participant in their teenage year (out of a total possible score of 42) is associated with a 2.6% increase in mathematics publications and a 4.5% increase in mathematics citations over their lifetime. The chance that an IMO gold medallist will become a Fields medallist is fifty times larger than the corresponding probability for a PhD graduate from a top 10 mathematics programme. We find that this is both because strong IMO performers are more likely to become professional mathematicians; and conditional on becoming professional mathematicians, they are more productive than lesser IMO performers, and are significantly more likely to produce frontier research in mathematics. We also show that this relationship reflects the underlying talent distribution and is not due to an effect of initial success of receiving a medal. For instance, we find no difference in lifetime performance of participants who ‘just’ made it to receiving a medal compared to those who nearly missed them.
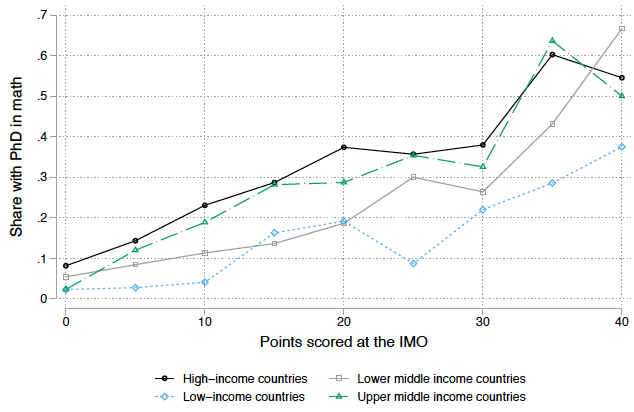
Figure 2 IMO results by share with a PhD in maths
Next, we find that compared to their counterparts from high-income countries who obtained the same score in the IMOs, participants born in low- or middle-income countries produce considerably less knowledge over their lifetime. A participant from a low-income country produces 35% fewer mathematics publications and receives over 50% fewer mathematics citations than an equally talented participant from a high-income country. The cross-country income group differences in mathematics knowledge produced in large part reflect differences in the propensity to get a PhD in mathematics. IMO participants from low- and middle-income are considerably less likely to do a PhD in their home country (and not more likely to do a PhD abroad). The lower propensity to earn a PhD at home is in turn correlated with the home country having weak mathematics research and training capacity.
What are the broader implications of losing a few talented individuals from developing countries? To answer this, first we estimate that the knowledge production could be 10% higher in terms of publications and 17% higher in terms of citations if developing country participants were not lost to the world of science. Second, we find that the loss is biggest for frontier research – such as those that are considered worthy of the Fields Medal. Third, we find that, for developing country medallists, the lower incidence of employment in mathematics academia is not offset by a greater propensity to be employed in non-mathematics academia, or in prominent industry positions. Instead, medallists from developing countries are more likely to become ‘invisible’ or at least not have any prominent careers.
Why are developing country participants less likely to become professional mathematicians and produce less mathematical knowledge? Research and training capacity in the home country seems to play a role. However, other factors may also be at play. For instance, developing country participants may have different preferences or private incentives to enter different types of careers, in particular if careers outside mathematics pay more. Future research may further elucidate the role of different factors in cross-country differences in the utilisation of talent. For now, we briefly mention several types of push programmes that could be useful in light of our findings:
- First, fellowships for high-end talent to study mathematics at undergraduate and/or graduate levels may alleviate resource constraints and make mathematics careers more attractive.
- Second, top schools could encourage applications from developing countries; and recruiting elite talent to their student programs is probably in their interest.
- Third, strengthening mathematics research and training capacity in developing countries could not only improve the training of those who prefer to stay in their home country, but would also make mathematics research careers more attractive to them.
While our research has focused on mathematics, there are other disciplines – such as biomedicine and computer science – where knowledge production is perhaps more immediately important for welfare. We suspect that developing country talent might also be underutilised in those fields. Our findings suggest that policies to encourage exceptionally-talented youth to pursue scientific careers – especially those from lower income countries – could accelerate the advancement of the knowledge frontier.
References
Agarwal, R and P Gaule (2018), “Invisible geniuses: Could the knowledge frontier advance faster?” IMF Working Paper 18/268.
Gessen, M (2009), Perfect rigor: A genius and the mathematical breakthrough of the century, Houghton Mifflin Harcourt.
Kremer, M and H Williams (2010), “Incentivizing innovation: Adding to the toolkit,” Innovation Policy and the Economy 10(1): 1–17.
Maurer, S M and S Scotchmer (2004), “Procuring knowledge,” in Intellectual property and entrepreneurship, Emerald Group Publishing Limited: 1-31.
Szpiro, G (2008), Poincare's Prize: The hundred-Year Quest to Solve One of Math's Greatest Puzzles, Penguin.
Stephan, P E (2012), How economics shapes science, Harvard University Press.
Overbye, D (2006) “Elusive proof, elusive prover: A new mathematical mystery,” New York Times, 15 August.
Williams, H, (2012), “Innovation inducement prizes: Connecting research to policy,” Journal of Policy Analysis and Management 31(3): 752–776.