As we are writing, the COVID-19 pandemic is still ongoing. Even though a vaccine is being deployed, the epidemic is expected to continue so policymakers are still facing tough containment strategy choices. As COVID-19 mortality increases with age, an obvious way to limit the death toll could come from controlling the number of potential infectious contacts of those with a higher probability of dying. Accounting for age heterogeneity in a combination of epidemiological and economic models is therefore key when assessing the potential payoffs and risks of different reopening strategies.
The susceptible-infected-removed-age macro model
Eichenbaum et al. (2020a, 2020b) (ERT henceforth) merge a basic epidemiological SIR (Susceptible-Infected-Removed) model with a macroeconomic framework. In a recent paper (Giagheddu and Papetti 2020), we extend this model by allowing for age-specific economic interactions, drawing from the epidemiological model of Towers and Feng (2012), thus developing a ‘SIR-age macro’ model. Our theoretical framework differentiates two age classes: retirees (those aged 70 or more) and the rest of the population (for simplicity labelled as young). The former group faces a 20-30 times higher probability of dying from COVID-19, in accordance with empirical studies (e.g. Goldstein and Lee 2020, Rinaldi and Paradisi 2020). As individuals do not internalise the aggregate effect of their economic decisions on the spread of the virus, it is optimal to adopt public containment measures. We consider two connected measures: (1) economic shutdown, for analytical convenience identified as a Pigouvian tax on consumption (like in ERT), rather than as a suspension of activities; and (2) social distancing, identified as an exogenous variation of the intra- and inter-generational contacts. The former makes consumption (hence production) more expensive and hence has a direct impact on economic activity. It can further be be directly managed by the public authority. The latter can be attributed not only to containment measures but also to behavioural changes unrelated to consumption and labour such as, for example, the adoption of personal protective equipment.
Comparing optimal economic shutdown and social distancing policies
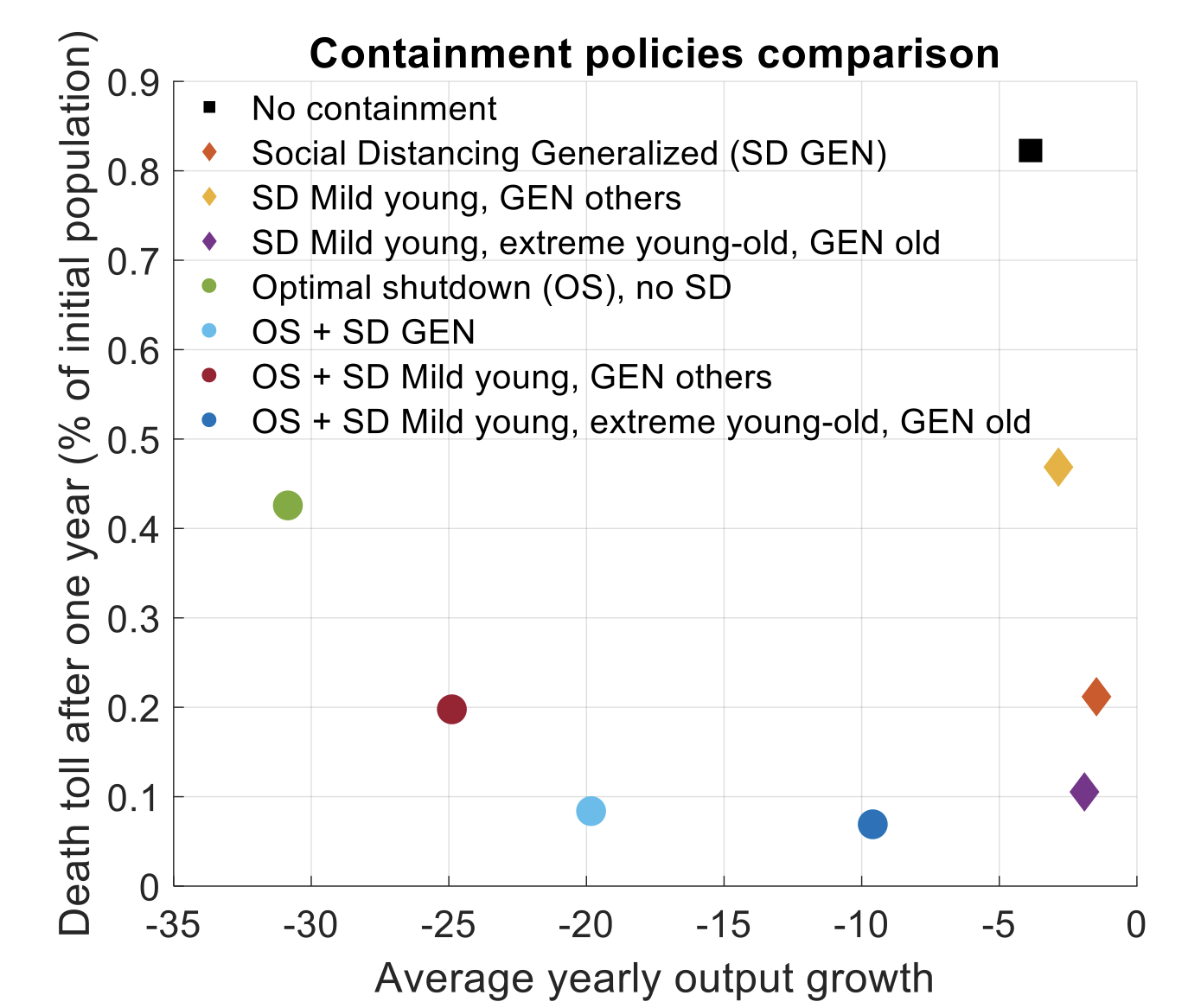
The model shows that for given social distancing, the optimal economic shutdown (based on maximising the welfare of all agents in the economy) is implemented from the beginning of the epidemic. Its duration and intensity increase with the intensity of the epidemic itself and with the time-proximity of the expected arrival of an effective vaccine. Furthermore, for a given economic shutdown, uniform social distancing measures are less effective compared with age-targeted measures. As shown in Figure 1, we see a reduction of deaths moving from generalised social distancing (orange diamond) to social distancing that is strictly imposed on retirees and only mildly imposed on young individuals. If there is an additional form of more extreme social distancing imposed between the young and the retirees, the death toll shrinks further (violet diamond). Adding the optimal economic shutdown on top of social distancing (dots in Figure 1), the cumulative GDP contraction is significantly less severe as the number of contacts between the retirees and the rest of the population is reduced. The basic intuition behind the result is that the retirees face a higher mortality risk and contribute less to economic activity. Meanwhile, the additional gain in terms of reduced deaths attained by the economic shutdown is meagre. Social distancing alone (if appropriately designed) can attain the same reduction in the death toll as an economic shutdown but with a much smaller reduction in output, as shown by comparing the diamonds with the dots in Figure 1. However, we recognise that our framework cannot capture potential costs arising from losing contact to other individuals.
Figure 1 SIR-age macro model containment policies comparison
Note: The optimal economic shutdown parameter (μc in the paper) is computed for the case in which a vaccine is expected to be discovered in one year time from the outbreak of the epidemic. The scenario ‘generalized (GEN)’ assumes that each social contact is diminished by 20% with respect to the baseline (no social distancing). The scenario ‘mild young, GEN on others’ is the same as GEN but the social distancing among young individuals is 50% less severe than in GEN. The scenario ‘mild young, extreme on young-old, GEN old’ is the same as the previous scenario but assumes that no contact is allowed between young and old individuals.
Bringing the model to the data: Reopening scenarios
We evaluate the model’s capacity to replicate actual data and the possible reopening scenarios after the ‘first wave’ of contagion, considering the case of Italy. We calibrate the model, including the containment policies, to target the number of excessive deaths and the output loss according to data and available estimates until 2 May 2020 (the day the Italian government started removing some containment measures after a lockdown phase and when we stopped retrieving data). As we manage to calibrate the model in line with the epidemic and economic developments, we evaluate the impact of hypothetical scenarios for a given rule governing the economic shutdown (we assume that the consumption tax adjusts in proportion to the contemporaneous number of total infected). We consider scenarios that differ depending on the type of social distancing:
- Uniformly (with respect to age) careful (as much as in the lockdown phase);
- Uniformly (with respect to age) less careful, reduced by 50% with respect to scenario 1;
- More careful with regards to inter-generational contact between retirees and the rest of the population (two-thirds less contact than in scenario 1); less careful with regards to intra-generational contact (two-thirds more contact than in scenario 1).
The results show that, under scenario 1 compared to the laissez faire equilibrium (where we assume the same number of contacts observed in pre-epidemic times according to Mossong et al. 2017), the final number of deaths due to COVID-19 is reduced by three, accompanied by a four times as large loss in GDP. Compared to scenario 1, the final death toll is approximately the same in scenario 3, with less deaths among the retirees, while it duplicates in scenario 2. The average reduction of real GDP in 2020 under the three scenarios is 8.6%, 11.4% and 10.6%, respectively. Higher losses are mostly attributable to the higher consumption taxes in response to the increasing number of total infected, as well as the reduced productivity of those young agents who get infected and their endogenous behavioural reaction on consumption and labour. Scenario 1 is relatively unfeasible and unrealistic as it assumes that the extremely strict lockdown phase in Italy which lasted until 2 May 2020, is implemented for the entirety of the year. Scenarios 2 and 3 are closer to the containment policies effectively implemented – with scenario 3 preferred as it leads to a lower death toll. However, both scenarios lead to a higher loss in GDP.
Concluding remarks
Our analysis suggests that it would be optimal to differentiate containment measures by age in order to limit the spread of COVID-19. Compared to uniform social distancing and generalized economic shutdown measures, age-targeted measures which especially limit the contacts between the elderly and the young, reduce the death toll while containing the output losses. Further, the closer the arrival of an effective vaccine, the more optimal is the implementation of a generalised economic shutdown. However, the stringency of the shutdown can be significantly mitigated by implementing age-targeted social distancing. Given the uncertainty surrounding many of the model parameters, we recognise that our quantitative results have to be taken with caution. Further, our analysis is not able to tackle important aspects such as the welfare and human costs of prolonged age-targeted social distancing; the limits imposed by the hospitalisation capacity; the possibility of targeted polices focusing on the revealed health status of individuals; or the time-varying nature of COVID-19 transmissibility.
References
Acemoglu, D, V Chernozhukov, I Werning and M D Whinston (2020) “A Multi-Risk SIR Model with Optimally Targeted Lockdown”, NBER Working Paper No 27102.
Brotherhood, L, P Kircher, C Santos and M Tertilt (2020), “An economic model of the COVID-19 epidemic: The importance of testing and age-specific policies”, CEPR Discussion Paper 14695.
Chikina, M andW Pegden (2020), “Modeling strict age-targeted mitigation strategies for COVID19”, PLoS ONE 15(7): e0236237.
Eichenbaum, M, S Rebelo and M Trabandt (2020), “The Macroeconomics of Epidemics", NBER Working Paper No 26882.
Favero, C A, A Ichino and A Rustichini (2020), “Restarting the economy while saving lives under Covid-19”, CEPR Discussion Paper 14664.
Giagheddu, M and A Papetti (2020), “The Macroeconomics of Age-Varying Epidemics”, Covid Economics 58: 22-56.
Goldstein, J R and R D Lee (2020), "Demographic Perspectives on Mortality of Covid-19 and Other Epidemics”, NBER Working Paper No 27043.
Gollier, C (2020), “Cost-benefit analysis of age-specific deconfinement strategies”, Journal of Public Economic Theory 22(6): 1746-1771 (pre-published in Covid Economics 24: 1-31).
Heathcote, J, A Glover, D Krueger and V Rios-Rull (2020), “Health vs. wealth: On the distributional effects of controlling a pandemic”, NBER Working Paper No. 27046.
Ichino, A, G Calzolari, A Mattozzi, A Rustichini, G Zanella, M Anelli (2020), “Transition steps to stop COVID-19 without killing the world economy”, VoxEU.org, 25 March.
Mossong, J, N Hens, M Jit, P Beutels, K Auranen, R Mikolajczyk, M Massari, S Salmaso, G S Tomba, J Wallinga, J Heijne, M Sadkowska-Todys, M Rosinska and W J Edmunds (2017), Polymod social contact data, Version 1.1.
Rampini, A A (2020), “Sequential Lifting of COVID-19 Interventions with Population Heterogeneity”, NBER Working Paper No 27063.
Rinaldi, G and M Paradisi (2020), “An empirical estimate of the infection fatality rate of COVID-19 from the first Italian outbreak”, medRxiv.
Towers, S and Z Feng (2012), “Social contact patterns and control strategies for influenza in the elderly”, Mathematical Biosciences 240:241–9.
Endnotes
1 Age heterogeneity with respect to the COVID-19 epidemic has been considered in a set of studies employing purely epidemiological models (Acemoglu et al. 2020, Chikina and Pegden 2020, Favero et al. 2020, Gollier 2020 and Rampini 2020) to which we add the modelling of economic choices on consumption and labor. Other studies have incorporated economic choices by age: Brotherhood et al. (2020) build a choice-theoretic heterogeneous-agent model to study the importance of age-specific policies and testing; Heathcote et al. (2020) discuss the age-dependent welfare effects of shutdown policies. Compared to the former we explicitly consider the empirical intergenerational contacts prevailing in normal times, tailoring the model to a specific country; compared to the latter we allow the infection likelihood to increase with consumption and focus on age-specific, rather than solely general, containment policies.