Country-pairs self-select in regional trade agreements (RTAs), and we know from Baier and Berstrand (2004) that this endogeneity of RTAs biases the estimation of the impact of RTAs within a gravity framework (signing an RTA between natural partners should have a higher impact). Also, more difficult deals deliver less – the economic impact of entering RTAs is inversely related to the duration of the negotiations (Tarlea 2018).
If RTAs are endogenously determined by country-pair-time economic characteristics, their occurrence can be predicted. Against this background, one would like to know:
- what country-pair characteristics shape the natural geography of trade agreement;
- what is the magnitude of the gains to be reaped from signing agreements between natural trading partners; and
- what would be the consequences of withdrawing agreements unjustified on economic grounds (there may be, indeed, sound political reasons).
The difficult part of the exercise is that beyond their impact on bilateral trade flows within the integrated region, such agreements have also a multilateral dimension (Anderson and van Wincoop 2003). What ultimately matters are relativetrade costs – for any two countries, signing a trade agreement will increase their relative trade costs vis-à-vis their other trading partners. General equilibrium effects of RTAs and associated welfare changes must accordingly be taken on board (Egger et al.2011).
In a recent paper, we operationalise an empirical framework aiming to predict which country-pairs should trade within RTAs based solely on economic determinants (Fontagné and Santoni 2018). This ‘natural’ geography of RTAs can be gauged against the actual one to provide an estimation of the economic consequences of a different geography of trade costs, closer to the predicted one.
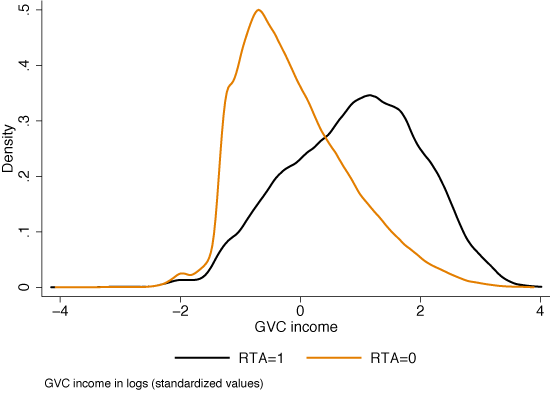
Among the economic determinants of an RTA, one should not miss the presence of global value chains (GVCs). Egger et al.(2008) was a first attempt to introduce the role of multinational and intra-industry trade as determinants of self-selection in RTAs. Now that methods and data addressing the intensity of the GVCs are available (Timmer et al.2013) one can shed new light on this determinant. Hence, the first take home is that GVCs (their actual intensity as measured by the value-added income) help predict RTAs. The fragmentation of production processes by multinational firms creates a ‘demand’ for a reduction in trade costs. Figure 1 reports preliminary evidence confirming that the bulk of value added trade occurs between countries with a preferential trade agreement in place.
Figure 1 Distribution of bilateral GVC income flows for country pairs within RTAs (RTA=1) or not (RTA=0)
Notes: Method developed by Timmer et al. (2013), applied to the EORA database for 189 countries.
Following Baier and Bergstrand (2004), our dependent variable is taking the value of 1 if the two countries in a pair are members of the same RTA in that year and zero otherwise. The occurrence of zeroes and ones is explained by usual economic determinants of the existence of RTAs – market size, similarity in economic size, comparative advantage, proximity of countries, number of agreements signed otherwise, and the bilateral value of GVC income within the two countries (all time-dependent variables are five years lagged). Considering 159 countries and thus 159x158/2 country-pairs over the period 1994-2015, our estimation confirms the role of usual determinants and the contribution of GVCs in predicting the occurrence of RTAs.
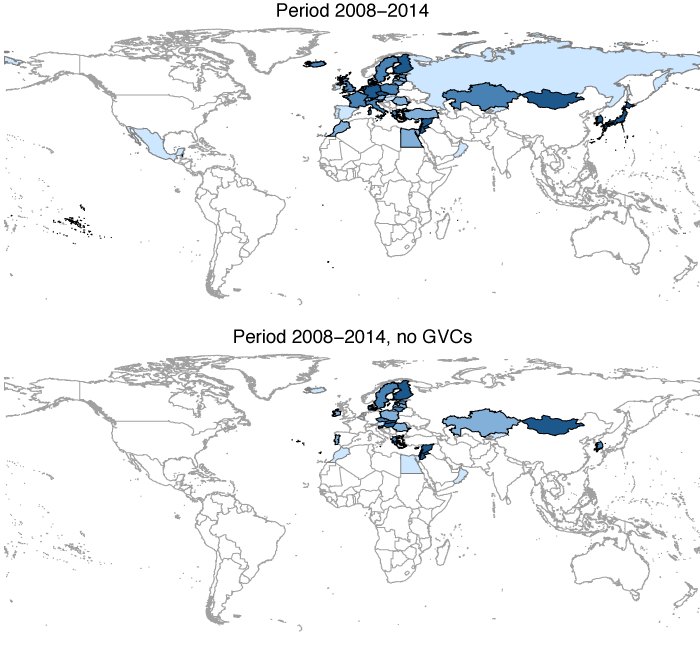
For sake of illustration, Figure 2 draws the map of RTAs predicted for China for the sub-period 2008-14, by taking on board (upper panel) or not (lower panel) the bilateral intensity of GVCs of China with its partners. It is evident that taking GVCs on board dramatically alters our vision of the natural geography of trade.
Figure 2 Natural trading partners of China, with and without GVC income as regressor (2008-14)
Note: Natural partners for China, i.e. with a probability above the relevant threshold. In the lower panel we predict RTAs probabilities imposing a marginal reduction in Chinese GVC participation by winsorizing the top 10% of bilateral GVC income. Nuances of blue reflect the probability of signing an RTA: a darker color indicates higher probability of signing.
Based on these estimates, as determined by country-pairs’ economic characteristics (including joint involvement in GVCs), one can predict the occurrence of RTAs, conditional on choosing the relevant probability threshold above which countries should sign-in. This threshold is not 50% indeed, as signing and not signing are not equiprobable.
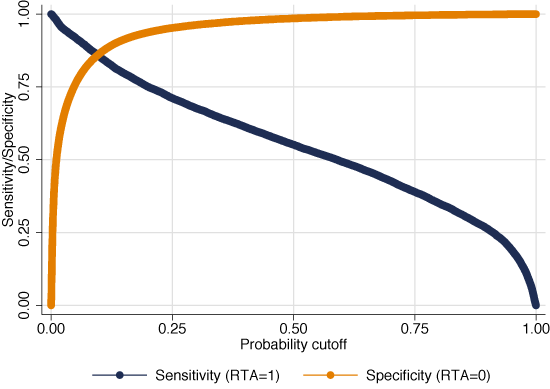
The chosen threshold optimises the trade-off between predicting correctly the undesirable agreements (‘specificity’), which is easy, and predicting correctly the actual RTAs (‘sensitivity’), which is more difficult. At the optimal cutoff (at the intersection of the two curves in Figure 3) our model correctly classifies 86% of positive RTAs and 80% of negative events for the overall period. Indeed, such a threshold is time-dependent, as the unconditional probability of being in an RTA increases on average over time. In the following, we split the sample period into three sub-periods and compute different thresholds for each.
Figure 3 Optimal cut off as determined by the sensitivity and specificity criteria
Note: Probabilities obtained from a Logit model for the period 1995-2014
Comparing predicted and actual RTAs gives four possible outcomes: true positives, true negatives, false negatives, and false positives. Among those, two cases are of special interest: the false negative when the model wrongly predicts the absence of an existing agreement, and the false positive when the model wrongly predicts an actually absent agreement. We can now use the list of false negatives and false positives to quantify the trade and welfare impacts of a change in the overall structure of trade costs, by changing the vector of signed (or not) agreements for each country pair.
In so doing, one must be cautious, however, that changing the bilateral structure of trade costs affects the entire matrix of trade costs worldwide (Head and Mayer 2014). Multilateral resistance terms (Anderson and van Wincoop 2003) can be considered as general equilibrium trade cost indexes that will vary as the new geography of bilateral trade costs is implemented. This is where structural gravity in general equilibrium is needed. We follow the procedure developed by Yotov et al.(2017) to derive general equilibrium effects from a structural gravity estimation. The procedure has four steps: a) solve the baseline gravity equation, b) define the counterfactual scenario, c) solve the counterfactual gravity model, and d) build the relevant general equilibrium indexes.
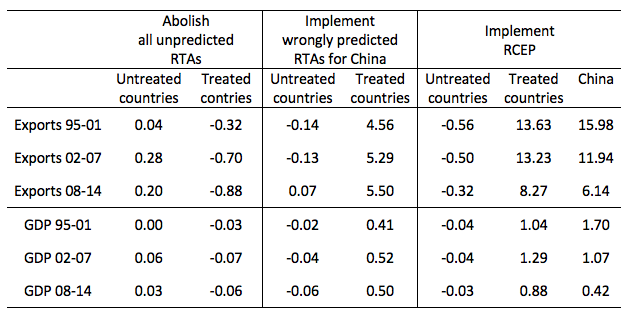
The first experiment is to withdraw country-pairs from all wrongly unpredicted RTAs. The false negatives at each date during the considered sub-period are withdrawn. As EU countries enter jointly in any new agreement, we adopt the rule of thumb of majority, and further consider that false negatives against the majority of member states are false negatives for the remaining ones as well. Interestingly, exiting from a sub-optimal agreement lead exiting countries to lose in terms of exports (their total exports decline by almost 1% in the last sub-period) – and marginally in GDP terms. The gains to be expected for third countries (due to the reversal of the trade diversion effects) are moderated. All in all, this suggests that RTAs originally at odds with the underlying economic determinants did significantly not divert world trade flows, once in place, and instead created conditions for (moderate) further trade expansion between participating countries.
Our second and third experiments focus on China. The country currently has RTAs with Australia, Costa Rica, Chile, Georgia, Iceland, New Zealand, Korea, Pakistan, Peru, Singapore, Switzerland, and APTA and ASEAN countries. We start by implementing the wrongly predicted RTAs. As shown in Figure 2, the EU and Russia are good candidates as soon as GVCs are considered. China would record a 5.5% increase in its total exports and 0.5% additional GDP. The magnitude of this effect is increasing over time. Notice also that the trade diversion effect vanishes for the most recent sub-period. Such non-trivial gains are in line with a new geography of RTAs predicted by the shift of the gravity centre of the world economy towards ‘Factory China’ and the associated involvement of China in GVCs involving partners beyond surrounding countries (Baldwin and Lopez-Gonzalez 2015).
Now consider the Regional Comprehensive Economic Partnership (RCEP), an initiative encouraged by China (Whalley and Li 2014). Interestingly, the impact on Chinese exports is much smaller in 2008-14 compared to 1995-01 or even 2002-07. This also translates into Chinese welfare gains divided by 4 if one compares 2008-14 with 1995-01. For other potential members of RCEP, the agreement has also lost interest, but mainly over the period 2008-14. In other words, the RCEP was an agreement worth signing beforethe negotiations started in November 2012. It is progressively becoming less relevant as Factory China is an increasingly global actor.
Table 1 Trade and GDP impacts of an alternative geography of RTAS
Note: Panel “abolish”: all wrongly unpredicted agreements (at each period) are removed. Panel “Implement wrongly predicted”: al wrongly predicted Chinese agreements (at each period) are enforced. Panel “RCEP”: members of the negotiations agree on the same RTA at each period. All changes in percent changes with respect to volume of total exports (or GDP) at the beginning of the considered period. Weighted mean of country level changes, using initial GDP as weight.
References
Anderson, J E, and E Van Wincoop (2003), “Gravity with gravitas: a solution to the border puzzle”, The American Economic Review (93): 170-192.
Baier, S L, and J H Bergstrand (2004), “Economic determinants of free trade agreements”, Journal of International Economics (64): 29-63.
Baldwin, R, and J Lopez‐Gonzalez (2015), “Supply‐chain trade: a portrait of global patterns and several testable hypotheses”, The World Economy 38(11): 1682-1721.
Egger, H, P Egger, and D Greenaway (2008), “The trade structure effects of endogenous regional trade agreements”, Journal of international Economics (74): 278-298.
Egger, P, M Larch, K E Staub, and R Winkelmann (2011), “The Trade Effects of Endogenous Preferential Trade Agreements”, American Economic Journal: Economic Policy (3): 113-43.
Fally, T (2015), “Structural gravity and fixed effects”, Journal of International Economics (97): 76 – 85.
Fontagné, L, and G Santoni (2018), “GVCs and the Endogenous Geography of RTAs”, CEPII Working Paper 2018- 05.
Head, K, and T Mayer (2014), Gravity Equations: Workhorse, Toolkit, and Cookbook, Elsevier, 131-195.
Tarlea F (2018), “The suspense of trade agreements”, VoxEU.org, 7 April.
Timmer, M P, B Los, R Stehrer, and G J Vries (2013), “Rethinking competitiveness: The global value chain revolution”, VoxEU.org, 26 June.
Whalley J, and C Li (2014), “China’s regional and bilateral trade agreements”, VoxEU.org, 5 March.
Yotov, Y, R Piermartini, J-A Monteiro, and M Larch (2017), “An Advanced Guide to Trade Policy Analysis: The Structural Gravity Model”, World Trade Organization.