“International macroeconomists know that the behavior of real exchange rates — exchange rates adjusted for relative inflation — is a prime piece of evidence for price stickiness. Not only do real rates move very closely with nominal rates, but the behavior of real rates changes dramatically when you move from floating to fixed rates or vice versa.”
Paul Krugman
The relative purchasing power parity (PPP) puzzle is one of the central puzzles in international economics. Movements in real exchange rates are large, persistent, and closely track movements in nominal rates, while cross-country differences in inflation rates are small and stable. Since at least the work of Mussa (1986), economists have often interpreted these observations as direct evidence for nominal price rigidities. More recently, a large academic literature has quantitatively evaluated whether sticky price open economy models can account for these observations, showing that variants of these models can generate the volatility and persistence of the real exchange rate that is observed in the data.
Using CPI microdata to evaluate the role of price stickiness
In a recent paper (Blanco and Cravino 2018), we challenge this view using a novel dataset containing the micro-price data that underlie the construction of the consumer price indices (CPIs) in five different countries. We use these data to construct a statistic that we label the ‘reset exchange rate’. It measures the cross-country relative price, in a common currency, of the subset of goods that exhibit a price change relative to the previous month. The reset exchange rate informs us whether nominal price rigidities are an important factor dampening the adjustment of prices to shocks affecting the nominal exchange rate. If they are not, the distinction between reset and non-reset prices should be irrelevant, and the reset and the real exchanges rate should move with each other. In contrast, if sticky prices are a primary factor dampening the response of inflation to exchange rate shocks, one would expect to see large differences between the real and the reset exchange rate movements.
Real and reset exchange rates in the data
We evaluate this central prediction of sticky price open economy models using the microdata that underlie the construction of the CPIs in Austria, Chile, Finland, Mexico, and the UK. These data contain monthly price quotes for uniquely defined products which can be traced through time. The combined dataset contains over 43 million monthly price quotes for the 2006-2015 period. To our knowledge, ours is the first study combining CPI microdata from multiple countries to study the behaviour of real exchange rates.
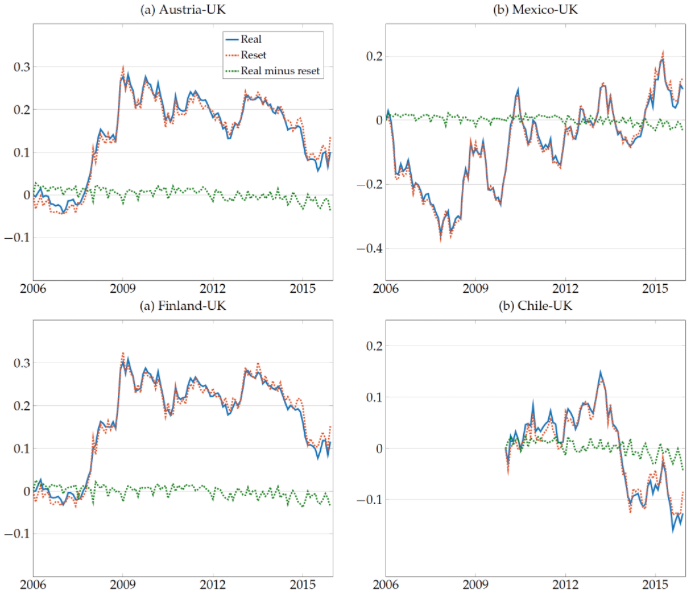
Figure 1 Empirical decomposition of the real exchange rate
Note: ‘Real’ and ‘Reset’ refer to the real and the reset exchange rates reset. The figure plots cumulative changes since January 2006 for Austria-UK, Mexico-UK and Finland-UK, and cumulative changes since January 2010 for Chile UK.
Figure 1 plots cumulative changes in real exchange rates, reset exchange rates, and in the difference between these two for each country relative to the UK. The figure shows that the real and the reset exchange rate are on top of each other. In particular, movements in the reset exchange rate are as large and are strongly correlated to those in real exchange rates.
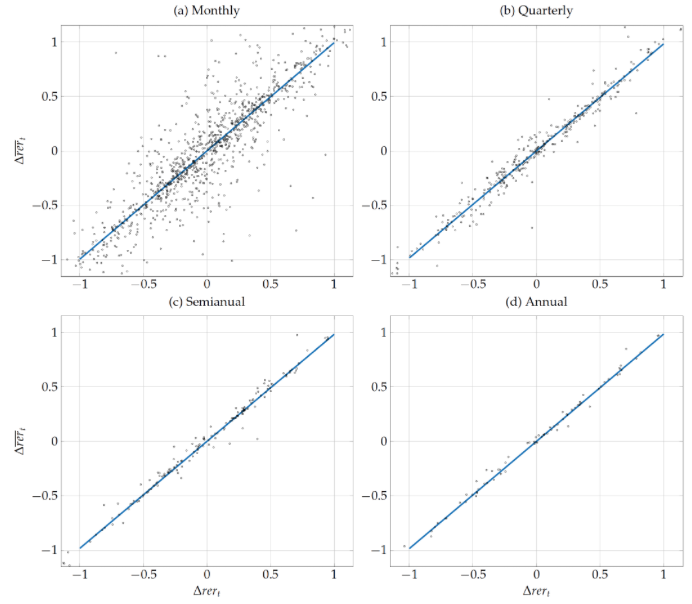
Figure 2 compares movements in the real exchange rates (x-axis) to changes in the reset exchange rates (y-axis), for changes computed at monthly, quarterly, semi-annual and annual frequencies. We pool all country-pairs into each figure, so that each point represents a country-pair in a given month/quarter/semester/year. We also normalise all changes by twice standard deviation of the real exchange rate to facilitate the comparison across country-pairs. The figure shows that the changes in the real and the reset exchange rate always line up around the 45 degree line,reflecting that the changes in these two variables go one to one with each other, independently of the frequency at which these changes are computed. This indicates that distinguishing between goods that did and did not change prices is of no consequence for understating the dynamics of the real exchange rate.
Figure 2 Changes in real versus reset exchange rates
Note: The figure plots changes in real exchange rates (x-axis) and changes in reset exchange rates (y-axis) computed at monthly, quarterly, semi-annual and annual frequencies. Changes in real and reset exchange rate are both normalized by two times the standard deviation of the change in the bilateral real exchange rate. Each circle represents a change for a country pair. A fitted line is depicted in solid blue.
Can sticky price models account for the behaviour of real and reset exchange rates?
A large literature has quantitatively evaluated whether sticky price open economy model can account for the observed dynamics in the real exchange rate. Our study asks whether these models can also account for the dynamics of the reset exchange rate. To do this, we analysed a workhorse new-Keynesian model with complete asset markets featuring real price rigidities and nominal wage stickiness, in the spirit of Chari et al. (2002) and the long literature that followed and is summarised by Engel (2018). We also evaluated the predictions of an incomplete market open economy model with financial shocks, in the spirit of Gabaix and Maggiori (2014) and Itskhoki and Mukin (2017).
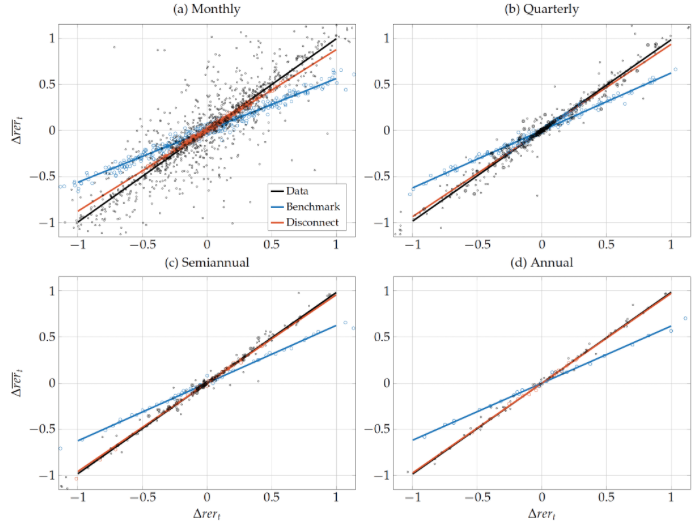
Figure 3 compares the movements in the real versus the reset exchange rates in the data and in the quantitative models. The figure shows that the complete markets models are incapable of generating large movements in the reset exchange rate. In contrast, the incomplete market models with financial shocks can generate movements in reset exchange rates that are in line with those observed in the data. Intuitively, forward-looking firms set prices to respond to current and expected future wages. In the complete markets models, even in the presence of nominal wage rigidities, relative wages expressed in a common currency mean revert quickly, so that future relative wages are not affected much by current shocks. In contrast, the incomplete market model can generate large and persistent movements in relative wages.
Our measure of reset exchange rates can be seen as a proxy for economy-wide relative costs, which are hard to measure directly in the data. Our analysis suggests that relative costs that are persistent and track the nominal exchange rate are needed to generate the observed movements in relative reset prices.
Taking stock
Addressing the PPP puzzle is one of the central questions in international economics. The microdata that underlies the construction of the CPI can shed light on this puzzle, as it allows us to isolate the real exchange rate for the subset of goods that change prices (which we label the reset exchange rate). The data show that reset and real exchange rate move one to one with each other. This observation presents a challenge for most workhorse sticky price open economy models that rely on sticky prices to generate large and persistent movements in real exchange rates. Even in the presence of strong pricing complementarities and nominal wage rigidities, these models cannot generate the large movements in reset exchange rates.
Figure 3 Changes in real versus reset exchange rates: Models versus data
Note: The figure plots movements in real exchange rates (x-axis) and changes in reset exchange rates (yaxis), for changes computed at monthly, quarterly, semiannual and annual frequencies. Each circle represents a change for a country pair. ‘Benchmark’ refers to data simulated from a quantitative sticky price model with complete markets. ‘Disconnect’ refers to data simulated from the incomplete markets model based on Itskhoki and Mukhin (2017).
References
Blanco, A, and J Cravino (2018),“Price rigidities and the relative PPP.” NBER Working Paper 24655.
Chari, V V, P Kehoe, and E McGrattan (2002),“Can Sticky Price Models Generate Volatile and Persistent Exchange Rates?” Review of Economic Studies 69(3): 533–63.
Engel, C(2016), “Real Exchange Rate Convergence: The Roles of Price Stickiness and Monetary Policy,” Working Paper, September.
Gabaix, X and M Maggiori (2015),“International Liquidity and Exchange Rate Dynamics,” The Quarterly Journal of Economics 130(3): 1369–1420.
Itskhoki, O and D Mukhin (2017),“Exchange Rate Disconnect in General Equilibrium,” NBER Working Paper 23401.
Mussa, M (1986),“Nominal exchange rate regimes and the behavior of real exchange rates: Evidence and implications,” Carnegie-Rochester Conference Series on Public Policy 25(1): 117–214.