A notion central to macroprudential policy is that exuberant phases of financial cycles – associated with extraordinary risk taking, buoyant asset prices and abundant credit provision – can eventually turn and trigger a ‘Minsky moment’, i.e. a collapse of risk-taking which generates a financial crisis. Such cyclical shifts between financial exuberance and crisis are often related to negative externalities caused by individual behaviour, ultimately bringing about high costs for the aggregate real economy (Martín et al. 2021). The objective of macroprudential policy is to limit such downside risks to financial and economic activity by implementing countercyclical policies aimed at mitigating negative externalities, for example by addressing the build-up of financial imbalances and enhancing the resilience of the financial system (Constâncio 2017).
A major challenge for policymakers is in calibrating their instruments – by balancing the medium-term benefits of containing systemic risk with the short-term costs for the economy. Quantifying the cost-benefit analysis is no mean feat. It requires policymakers to formulate an explicit financial stability objective, to build an econometric model incorporating the sharp asymmetries between real and financial variables triggered by financial crises, and to quantify the cost of policy actions in the form of foregone economic growth.
A novel empirical framework to assist policymakers
The risk management approach we propose in Chavleishvili et al. (2021a and 2021b) offers an empirical framework to quantify such macroprudential trade-offs. It first broadens the notion of downside risk by considering the entire left tail of the GDP growth distribution, rather than just a specific quantile. Next, it relates the mean outlook for economic growth to its downside tail risk within a decision-theoretic framework. Finally, the framework estimates these quantities using a quantile vector autoregressive model that automatically incorporates any asymmetries present in the data.
First, the idea of downside risk is captured by the concept of ‘growth shortfall’. Growth shortfall extends the well-known notion of growth-at-risk, as applied in Adrian and Liang (2016), Cecchetti and Schoenholtz (2018), and Adrian et al. (2019), to the entire lower tail of the growth distribution. Growth-at-risk measures indicate the forecast growth associated with an arbitrarily chosen low probability of, say, 5%. Growth shortfall instead considers the entire expected lower tail below a threshold and can be thought of as the average of all quantiles below this value. The growth shortfall is closely related to stress testing and early warning crisis estimates, as it transfers the bank stress test concepts of ‘Loss Given Default’ and ‘Probability of Default’ to the macro-financial context. Indeed, in our macro-financial context GDP losses from growth contractions represent Loss Given Default and the probability of a contraction in GDP represents Probability of Default. The growth shortfall further relates to early warning studies of financial crises which focus especially on the likelihood of severe contractions caused by disruptions in the financial system (e.g. Schularick et al. 2021).
Second, growth shortfall needs to be integrated into a macroprudential objective function. Our proposed objective function transposes the risk-return concept from portfolio management or asset pricing to macroeconomic growth (see Carney (2020) for related insights, and Suarez (2021) for a micro-foundation of analogous objective functions). By activating available macroprudential instruments, the macroprudential policymaker maximises discounted future expected mean growth adjusted for downside risk. The policymaker balances expected growth with a preference-weighted measure of downside risk in the growth distribution over a policy-relevant time horizon.
Estimating macro-financial asymmetries
The third element of our framework is the estimation of amplification and propagation effects that generate the large real costs associated with financial crises. We advocate the use of a quantile vector autoregressive (QVAR) model fitted to euro area data, building on Cecchetti and Li (2008), White et al. (2015), and Chavleishvili and Manganelli (2019). The empirical model includes real GDP growth representing the business cycle, a broad-based financial cycle indicator measuring financial vulnerabilities, and a composite indicator of systemic stress (CISS) – developed by Holló et al. (2012) – capturing financial stress. The QVAR framework not only estimates the average direct and indirect interactions between all three variables, but also potentially differing tail dynamics.
The estimation results for the euro area confirm previously identified non-linearities (see e.g. Adrian et al., 2019) and highlight new propagation channels. Figure 1 visualises these results in terms of quantile impulse response functions. The response functions trace the transmission of a given innovation to selected quantiles of the endogenous variables, over 20 quarters. For instance, an unexpected increase in the variable for financial stress (in column 3) has a strong impact on the left tail of GDP growth, represented by the 10th percentile (in row 1, column 3), but has little impact on the median or upper tail of the growth distribution.
Figure 1 Quantile impulse response functions|
(horizontal axis in quarters)
Notes: Impulse responses of quantiles of GDP, financial cycle and systemic stress (CISS) to an unanticipated increase (innovation) in each of the variables. For instance, a sudden deterioration of systemic stress produces a contraction of 20 basis points of the 10th percentile of GDP but has no effect on the median and 90th percentile (row 1, column 3). As another example, unexpected positive news on euro area GDP contributes to reducing elevated systemic stress more strongly, as evidenced by the substantially more pronounced downward shift in the 90th percentile (row 3, column 1).
In addition, the quantile impulse response analysis reveals a vicious circle in the form of an adverse feedback loop between the financial cycle and systemic stress in times of crisis. A sudden contraction (negative innovation) of the financial cycle further increases systemic stress in a situation when stress is already elevated (row 3, column 2). The loop is completed by the fact that an adverse shock to the composite indicator of systemic stress (CISS) depresses the entire distribution of the financial cycle (row 2, column 3). The implication of this result is that, in periods of elevated stress, policy interventions that maintain favourable financial conditions avoid the risk of further amplification of the stress. Conversely, actions aimed at containing systemic stress contribute to improving financial conditions and mitigate the downside risk to the economy. If left unchecked, such feedback effects could amplify initial shocks into a full-blown crisis.
Stress testing
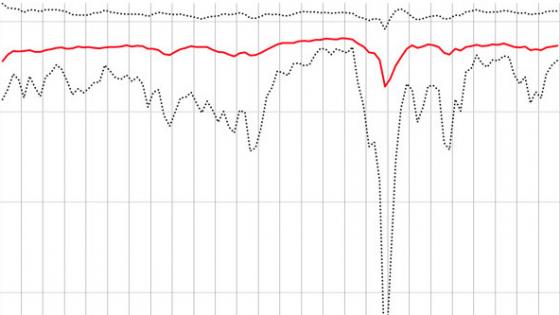
A complementary way to assess the impact of such an amplification mechanism on downside risks to the economy is through a macro-financial stress test. Stress tests can be designed in different ways. Figure 2 shows the impact the Global Crisis would have had on euro area GDP at each quarter of the available time series. It is constructed by extracting from the QVAR system the sequence of quantile realisations that as of 2008Q2 produced the GDP contraction observed in 2009Q2 at the onset of the Global Crisis. It next applies this same sequence of quantile realisations at each quarter and reports the ensuing GDP contraction.
Figure 2 Euro area resilience to GFC-like stress using a macro-financial stress test
Notes: Annual GDP growth as per historical data (dashed line) and as counterfactual under GFC-like stress (solid line). The counterfactual is constructed by extracting from the estimated model the sequence of quantile realisations that as of Q2 2008 produced the GDP contraction observed in Q2 2009 at the onset of the GFC. It next applies this same sequence of quantile realisations at each quarter and reports the ensuing GDP contraction. Horizontal lines refer to 10th, 50th and 90th empirical percentiles.
A few interesting facts are worth discussing. By design, stressed GDP (the continuous line) as of 2008Q2 is equal to realised GDP (the dashed line) as of 2009Q2. The stress test would however have been signalling risks as early as 2007, and the chart shows that the situation continued to be fragile until the euro area sovereign debt crisis (2011-2012). The comparison with the 1992 recession is particularly striking: even though GDP contracted for three consecutive periods, and by more than during the euro area sovereign debt crisis, the euro area economy was not vulnerable to a global financial crisis type of scenario. Macro-financial stress tests of this type can serve as a useful monitor for policymakers to detect downside risks in real time and, if necessary, take mitigating actions.
From stress testing to a macroprudential policy stance
We use our estimated QVAR model together with our macroprudential objective function to quantify a policymaker’s intertemporal trade-off, with the aim of pre-emptively curtailing the financial cycle in exuberant times. Specifically, we address the question: when could it be worthwhile to manage the financial cycle to reduce future tail risks?
The thought experiment compares a ‘passive’ macroprudential policy strategy with an ‘active’ one that tightens policy in the short run and loosens it at a later stage in crisis times (see Chavleishvili et al. (2021) for details). The passive macroprudential policy assumes higher values for the financial cycle over an initial exuberant phase of six quarters, followed by a subsequent crisis phase of six quarters with subdued values for the financial cycle. The active macroprudential policy tightens the financial cycle by ten percentiles during the exuberant phase but loosens it in the subsequent six crisis quarters by ten percentiles to support financial intermediation.
This mimics the strategy for the countercyclical buffer, which involves increasing the buffer well ahead of mounting imbalances in the banking sector, thereby offering support for a sustainable provision of credit to the real economy in a potential downturn. Contrary to reality, however, our counterfactual experiment assumes a fixed time period of six quarters for the onset of the crisis. It further implicitly assumes that policymakers are effective in supporting the financial cycle by loosening macroprudential measures in crisis times. This simplification allows us to focus on the intertemporal trade-off.
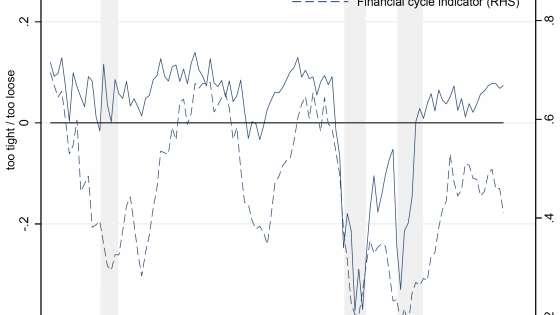
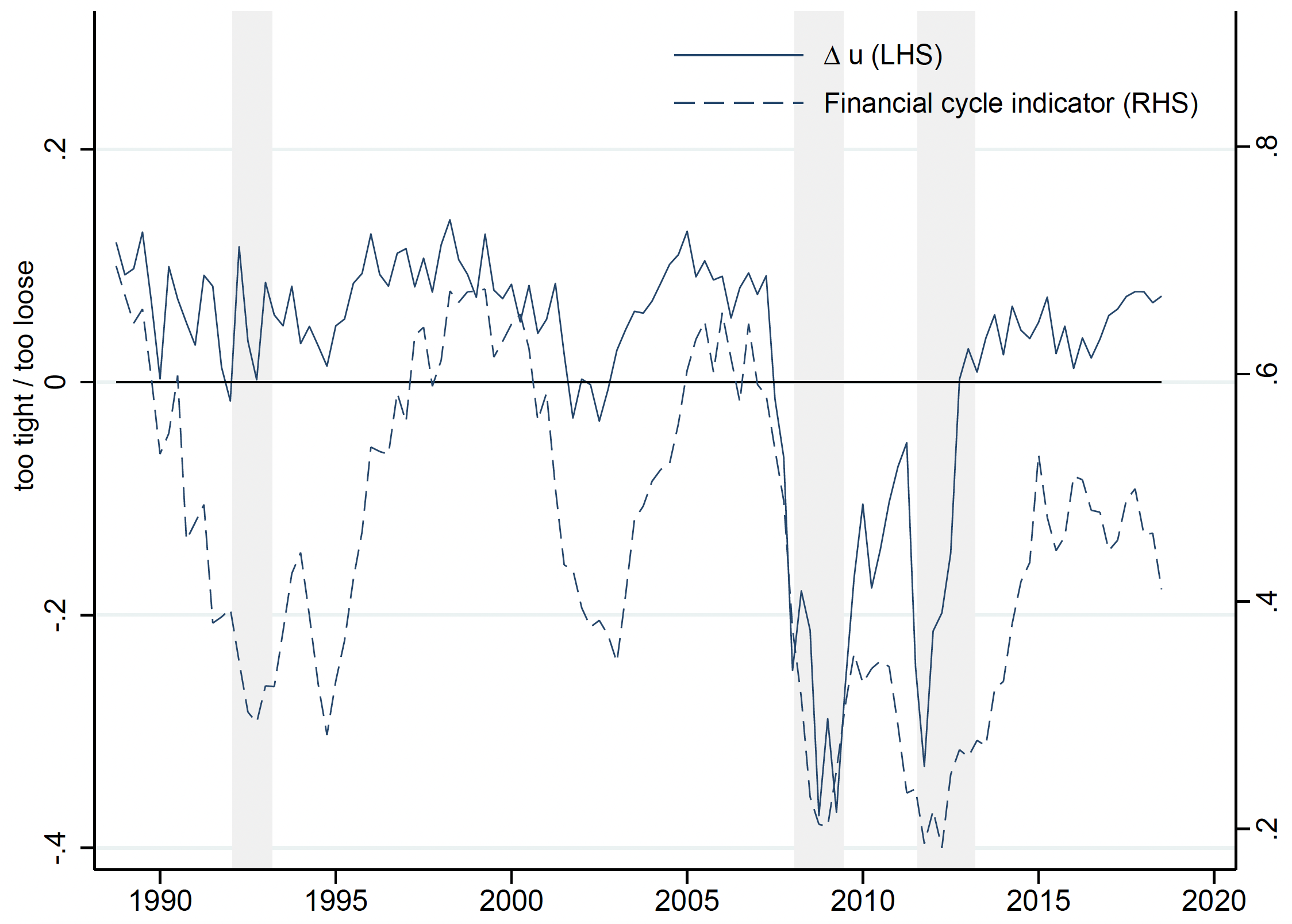
We consider the macroprudential stance as the difference in the resulting macroprudential objective function between the active (countercyclical) and the passive macroprudential policy. If the difference, labelled as 'Δu' in Figure 3, is positive, there are expected gains from the active policy by initially moderating the financial cycle, subsequently supporting financial intermediation after a crisis has hit.
For the euro area, the net benefits from actively leaning against the financial cycle are positive most of the time (see the solid line in Figure 3). The experiment shows that the benefits would have been largest during the buoyant conditions in the late 1990s before the bust of the dot-com boom in 2000, and during the mid-2000s before the onset of the Global Crisis in 2007. But an additional tighter policy during 2008-2009 or during the euro area sovereign debt crisis in 2011-2012 would have amplified downside risks as the financial system was already deleveraging. The macroprudential stance metric offers an indication to policymakers as to when there is scope for pre-emptively tightening macroprudential conditions to stabilise macroeconomic outcomes.
Figure 3 Net gains from countercyclical macroprudential policy
Notes: The solid line indicates net benefits of adopting an actively countercyclical macroprudential policy based on a specific objective function, relative to a passive policy. It is constructed as the difference (u) between the expected utility associated with the active policy (tightening macroprudential instruments during the expansion and releasing them during crises) and the passive policy (which does not act countercyclically). The dashed line is the observed time series of the financial cycle. Although our stance metric is correlated with the financial cycle (dashed line), such correlation is not perfect. For example, the recessions of the early 1990s and 2000s were accompanied by a subdued financial cycle, but the stance metric would have provided only limited indications that macroprudential measures should be loosened. In contrast, the subdued financial cycle following the global financial crisis was accompanied by a macro-financial constellation that would have argued for stronger support of GDP growth from looser financial conditions.
The stance metric is mildly correlated with the euro area financial cycle, suggesting that the financial cycle itself is a valuable variable to inform macroprudential policy discussions about potential financial imbalances in real time. The financial cycle is, however, not perfectly correlated to the stance. For example, the recessions of the early 1990s and 2000s were accompanied by a subdued financial cycle, but the stance metric would have provided only limited indications that macroprudential measures should be loosened. In contrast, the subdued financial cycle following the Global Crisis was accompanied by a macro-financial constellation that would have argued for stronger support of GDP growth from looser financial conditions.
Our thought experiment demonstrates how our proposed framework may help macroprudential authorities systematically and consistently assess the case for ‘leaning against the wind’ policies – i.e. a preventive tightening of macroprudential policy in good times, well ahead of a potential downturn, in line with the arguments for macroprudential space (de Guindos 2021).
Conclusions
The proposed risk management approach to macroprudential policy quantifies the trade-off between containing tail risks to economic activity and facilitating expected growth. Our empirical QVAR framework offers the additional advantage of complementing the basic growth-at-risk setup – which builds on the short-term ability of financial stress (or financial conditions) to predict tail growth risks – with an amplification mechanism through financial vulnerabilities. It does so without relying on the long-term ability of vulnerability indicators to predict future financial crises, which is typically the focus in the ‘early warning’ literature. The macro-financial stress test and the counterfactual exercise on the macroprudential stance are two readily available tools that policymakers can use to assess underlying vulnerabilities and assess the opportunity for adjusting macroprudential instruments.
Authors’ Note: This column first appeared as a Research Bulletin of the European Central Bank. It features research-based analysis conducted within the ECB’s Research Task Force on monetary policy, macroprudential policy and financial stability. The authors gratefully acknowledge comments and suggestions from Alexander Popov and Zoe Sprokel. The views expressed here are those of the authors and do not necessarily represent the views of the European Central Bank, the Eurosystem, or the European Commission.
References
Adrian, T, N Boyarchenko and D Giannone (2019), “Vulnerable growth”, American Economic Review 109(4): 1263-1289.
Adrian, T and N Liang (2016), “Monetary policy, financial conditions, and financial stability”, VoxEU.org, 14 August.
Carney, M (2020), “The grand unifying theory (and practice) of macroprudential policy”, speech at University College London, 5 March.
Cecchetti, S G and H Li (2008), “Measuring the impact of asset price booms using Quantile Vector Autoregressions”, unpublished manuscript.
Cecchetti, S G and K Schoenholtz (2018), “GDP at risk”, VoxEU.org, 11 January.
Chavleishvili, S, R F Engle, S Fahr, M Kremer, S Manganelli and B Schwaab (2021a), “The risk management approach to macroprudential policy”, Working Paper Series No. 2565, European Central Bank.
Chavleishvili, S, S Fahr, M Kremer, S Manganelli and B Schwaab (2021b), “A risk management perspective on macroprudential policy”, Working Paper Series No. 2556, European Central Bank.
Chavleishvili, S and S Manganelli (2019), “Forecasting and stress testing with quantile vector autoregression”, Working Paper Series No 2330, European Central Bank.
Constâncio, V (2017), “Macroprudential stress tests: A new analytical tool”, VoxEU.org, 22 February.
De Guindos, L (2021), “Macroprudential policy after the COVID-19 pandemic”, Panel contribution at the Banque de France / Sciences Po Financial Stability Review Conference 2021, 5 March.
Holló, D, M Kremer and M Lo Duca (2012), “CISS – a composite indicator of systemic stress in the financial system”, Working Paper Series No 1426, European Central Bank.
Martín, A, C Mendicino and A van der Gothe (2021), “On the interaction between monetary and macroprudential policies”, Working Paper Series No 2527, European Central Bank.
Schularick, M, L ter Steege and F Ward (2021), “‘Leaning against the wind’ and the risk of financial crises”, VoxEU.org, 12 January.
Suarez, J (2021), “Growth-at-risk and macroprudential policy design”, CEMFI mimeo.
White, H, T-H Kim and S Manganelli (2015), “VAR for VaR: Measuring tail dependence using multivariate regression quantiles”, Journal of Econometrics 187: 169-188.