It is a truism of Brexit commentary that in Parliament there is no majority for any outcome. Indeed, in the three ‘meaningful votes’ and twelve ‘indicative votes’ held earlier this year, not a single motion was passed by the House of Commons. As emphasised by Aidt et al. (2019), however, the relevant type of question for MPs is not whether they support any particular proposal in isolation – as against continued deliberations and an uncertain future – but rather which of two well-defined outcomes they prefer.
Questions of the latter sort would effectively be asked of parliamentarians if Brexit were to reach the ‘endgame’ stage; with a genuinely hard deadline approaching, with a manifestly unamendable withdrawal agreement on the table, and with a known legal default outcome in place. At some point sufficiently close to decision time, it would become apparent to MPs that declining to support one option was tantamount to actively supporting another, and that implicitly comparing outcomes had therefore become unavoidable.
Outcomes and preferences in the endgame
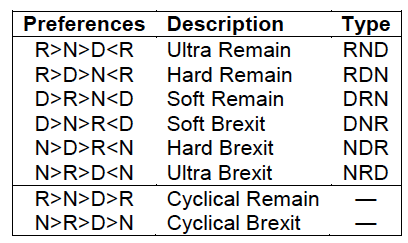
In the Brexit endgame, the only possible outcomes are to revoke Article 50 and remain in the EU (“R”), to leave on the basis of a specified withdrawal agreement ‘deal’ (“D”), or to leave with no deal (“N”). These three outcomes lead to the individual preference types in the first six rows of Table 1.
Table 1 Preference configurations
Here Remainers prefer outcome R to outcome N (written R>N), and Brexiteers have the opposite view (N>R). Moreover, preferences are described as soft, hard, or ultra according to whether outcome D is in first, second, or last position. Thus, for example, hard Remainers have the preference ranking R>D>N, abbreviated as type RDN.
If we knew the type of each voting MP, it would be simple to aggregate the three pairwise comparisons and determine the majority preferences in Parliament. Collectively, members might then display any of the eight configurations in Table 1. If the preferences of the group appear in one of the first six rows of the table, then the top-ranked outcome has majorities over both alternatives. An outcome with this property is called a ‘Condorcet winner’ (Condorcet 1785), and we may reasonably conjecture that such a winner will prevail in the endgame regardless of the fine details of the deliberation procedure (such as the sequencing of votes). On the other hand, if the majority exhibits one of the ‘Condorcet cycle’ preference patterns in the last two rows of the table, then we may conclude that procedural control confers substantial power to affect the result and that the legal default outcome is in an advantageous position.
Imputing preferences to parliamentarians
But how, prior to the endgame, can we attribute a preference type to each individual MP? In a recent paper (Tyson 2019), I construct a fully articulated model of parliamentary preferences by assigning types in the following way.
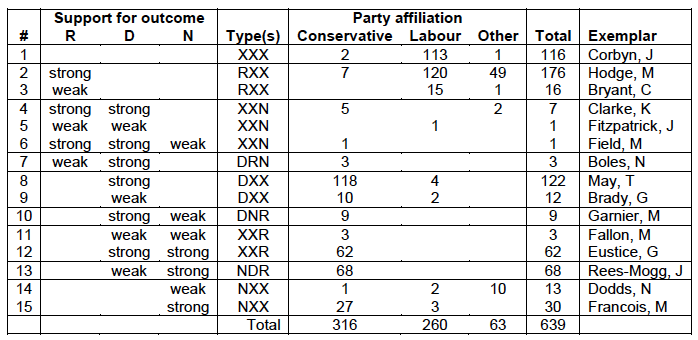
The first step is to use the meaningful and indicative votes to reveal which members have demonstrated support for one or more of the three outcomes. For each of R, D, and N, two Commons motions are selected that embody different levels of enthusiasm. For example, endorsing the withdrawal agreement on the first meaningful vote shows early, and hence strong, support for outcome D, while waiting for the third meaningful vote to give one’s backing indicates more reluctant, and hence weaker, support.1 Parliament can then be divided into coalitions of MPs with the same voting profile on all six selected motions, and for each such coalition I impose the baseline assumption that strong support for an outcome implies a higher preference than weak support, which in turn implies a higher preference than no support. The resulting coalitions and implied preference types are summarised in Table 2 (where “RXX” denotes either RND or RDN, and likewise for other type combinations).
Table 2 Voting coalitions and implied preference types
Here, Coalition 7 ranks D first (strong support), R second (weak support), and N last (no support). Coalition 9 must also rank D first (weak support), but can rank R and N in either order (both no support). Notably, there are no implications at all for the preferences of Coalition 1, which shows no support for any outcome by the selected measures.
Next, I supplement the baseline assumption with a number of more subjective political assumptions that further constrain the preferences of particular voting coalitions. For instance, if we are willing to assume that there are no (or negligibly few) ultra Remain MPs, then it follows that Coalitions 2–3 can be assigned type RDN.2
Finally, I define three parameters to control the more difficult political judgements necessary to complete the model: w for the number of soft Brexiteers (DNR) in Coalition 1; x for the number of soft Remainers (DRN) in Coalitions 1 and 4–6; and y for the number of soft Remainers in Coalitions 8–9. Any assignment of values to these parameters will yield a majority preference pattern, which will in turn have implications for the endgame.
Putting the model to work
The conclusions that can be drawn from this model are easily stated. First, outcome D has an enormous majority over outcome N for any parameter settings, and hence N cannot be a Condorcet winner. This fact gives a precise meaning to the common assertion that “there is no majority in Parliament for a no-deal Brexit”. However, it does not in itself guarantee anything about the endgame, as there may be no Condorcet winner at all.
Second, outcome D has a majority over outcome R if there are not too many hard Remainers in Coalitions 1 and 4–6.3 More precisely, such a majority arises if w plus x is at least 41, and in this case D is a Condorcet winner. Since Coalition 1 (which includes J Corbyn) is by far the largest of those relevant to this comparison, the prospects for outcome D in the endgame are seen to depend crucially on the preferences of a group of Labour loyalists.
Third, outcome R has a majority over outcome N if the number of soft Brexiteers in Coalition 1 is no more than the number of soft Remainers in Coalitions 8–9. The latter condition is just the statement that w does not exceed y, and in this case R is a Condorcet winner whenever D is not one. Since Coalition 8 (which includes T May) greatly outnumbers Coalition 9, the comparison between R and N thus amounts to a clash between moderate elements within the Labour and Conservative loyalist contingents.
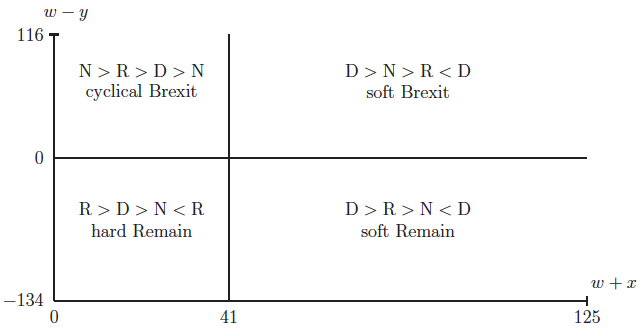
These conclusions are depicted graphically (and more concisely) in Figure 1. Here D is a Condorcet winner in the northeast and southeast quadrants, R is a Condorcet winner in the southwest quadrant, and the cyclical Brexit majority preference configuration appears in the northwest quadrant.4
Figure 1 Majority preferences in the parameterised model
May the best outcome win
Admittedly, the above algorithm for assigning types to MPs is somewhat rudimentary, and precise quantitative conclusions derived from the model may be regarded with due caution. Qualitatively, however, the conclusions reached should be robust to a considerable amount of error at the individual level. In particular, something resembling the landscape of majority preferences in Figure 1 will result from most plausible variations of the present calibration exercise.
So then, qualitatively speaking, what do practical politicians contemplating the Brexit endgame have to learn from this model of Parliament? The first and most obvious lesson is that D will easily prevail over N in any head-to-head contest. (The fact that the meaningful votes all failed then indicates that no deal was not seen as the eventual consequence of rejecting the withdrawal agreement.) Proponents of a deal should therefore concentrate on building a majority over R, with special attention to mainstream Labour MPs in Coalition 1 who may be convinced to behave as soft Remainers. The overwhelming strength of D against N also suggests that the status of no deal as the legal default outcome could conceivably help to pass a withdrawal agreement, if a last-gasp vote were to be held on the cusp of the deadline.
Another lesson is that, unlike its rivals, outcome R must fight battles on two different fronts. Remain advocates will need to target both mainstream Labour and mainstream Conservative members, recruiting both hard and soft Remain MPs as appropriate for the two necessary majorities. While the political challenges here appear to be formidable, the model does not exclude R emerging as the clear winner in terms of majority preferences.
A third lesson is that a fundamentally unstable, Condorcet-cycle scenario is a distinct possibility. If such a preference configuration occurs it will be of the cyclical Brexit variety, and this offers the only realistic opportunity for no deal to come through – by default – as the result of the endgame. Paradoxically, backers of N must defeat R in the struggle for moderate opinion in Parliament, but they cannot allow the prospect of remaining in the EU to vanish entirely since N would then be left defenceless against D.5 In this sense N can be seen as parasitic on R, depending on its host temporarily for survival but prepared to discard it when the time is right. This plan may be the hardest of all to execute successfully, but no miracles are required and hence the model does not support the claim that Parliament will never allow a no-deal exit.
References
Aidt, T, J Chadha and H Sabourian (2019), “Breaking the Brexit impasse: Achieving a fair, legitimate and democratic outcome”, VoxEU.org, 11 January.
Condorcet, M J A N, marquis de (1785), Essai sur l’application de l’analyse à la probabilité des décisions rendues à la pluralité des voix, Paris: Imprimerie Royale.
Hanretty, C (2017), “Areal interpolation and the UK’s referendum on EU membership”, Journal of Elections, Public Opinion and Parties 27: 466–483.
Tyson, C J (2019), “Meaningful votes, indicative votes, and the parliamentary Brexit endgame”, working paper.
Endnotes
[1] Similarly, support for R is shown by the indicative votes on “revocation of Article 50” (strong) and “parliamentary supremacy” (weak), while support for N is shown by the motions proposing to “leave with no deal” (strong) and to pursue “contingent preferential arrangements” (weak).
[2] Two further subjective assumptions are that all hard Brexiteers show weak support for D (like Coalition 13), and that all ultra Brexiteers show some support for N (like Coalitions 14–15). All three of these assumptions are imposed primarily for convenience, to simplify the model at the cost of little useful generality. (The model could, for example, accommodate a sizable number of ultra Remain MPs with no change to the aggregate conclusions.)
[3] Taking the analysis one step further, we could hypothesise that the members of Coalitions 1 and 4–6 most inclined to be hard Remainers are those whose constituents supported Brexit least in the 2016 referendum. Using the constituency-level Leave shares calculated by Hanretty (2017), it would then be possible to form a rough estimate of which specific MPs are pivotal for the majority preference between D and R.
[4] For the simplest example generating the majority preference dynamics in Figure 1, consider the following three-member parliament: Alice is classified as XXN, Bob as DXX, and Charlie as NRD. If Alice is in fact type DRN (east), then outcome D is a Condorcet winner. If Alice is RDN (west) and Bob is DRN (south), then R is a Condorcet winner. Finally, if Alice is RDN and Bob is DNR (north), then we obtain the cyclical Brexit pattern.
[5] In a Condorcet cycle situation, all three outcomes must continue to be achievable procedurally to sustain the instability. Under cyclical Brexit, if some extra-parliamentary force (such as the EU itself) were to make R infeasible, then N would lose its advantage – despite persisting as the legal default – and would succumb in a direct comparison against D.