Social scientists increasingly use confidential data held by government agencies or private firms to publish statistics based on small samples, from descriptive statistics on income distributions and health expenditures in small areas (e.g. Cooper et al. 2015, Chetty et al. 2018) to estimates of the causal effects of specific schools and hospitals (e.g. Angrist et al. 2013, Hull 2018). Such statistics allow researchers and policymakers to answer important questions. But releasing such statistics also raises concerns about privacy loss – the disclosure of information about a specific individual – which can undermine public trust and is typically prohibited by law in government agencies and user agreements in the private sector.
In order to address these challenges, a recent literature on ‘differential privacy’ methods, which has its roots in computer science and cryptography, has developed a suite of new methods that reduce privacy risks by adding a small amount of random noise to each estimate that is released. This approach permits precise statements about the privacy loss from any given release, and by varying the magnitude of the noise added, one can quantify the trade-off between privacy loss and accuracy.
As part of a collaboration with the US Census Bureau and researchers from the Harvard Privacy Tool Project, we adapted tools from the differential privacy literature to release the Opportunity Atlas, which provides estimates of upward mobility for each Census tract (neighbourhood) in the US. Although our main focus in that work was on analysing the statistics themselves, the disclosure method we developed to release those statistics may be valuable to other researchers who seek to release statistics based on small samples. Here, we describe how the methods we developed work and how they can be adapted to other applications.
Our method – which adds noise to each statistic in proportion to its sensitivity to the addition or removal of a single observation from the data – can be used to release arbitrarily complex statistics estimated using small samples. Intuitively, our approach permits the release of statistics in arbitrarily small samples by adding sufficient noise to the estimates to protect privacy.
Our approach is simple to implement and outperforms a number of widely used approaches that are currently used by researchers and government agencies to protect privacy, such as the omission of cells with very few observations from data releases. In particular, our approach reduces both privacy loss and statistical bias relative to such methods, with only a small sacrifice in statistical precision of the estimates.
The remainder of this column describes our method in more detail and illustrates how it was used to release estimates of social mobility by Census tract in the Opportunity Atlas. We provide a more complete treatment in our recently released paper (Chetty and Friedman 2019). We also provide a step-by-step guide and illustrative Stata code to implement our approach.
For concreteness, we focus on the problem of releasing estimates from univariate ordinary least squares (OLS) regressions estimated in small samples (e.g. small geographic units). We consider the case where the dataset can be broken into many groups (‘cells’) and one is interested in releasing statistics for one or more of these cells. For example, we may be interested in disclosing the predicted values from a regression of children’s income percentile ranks in adulthood on their parents’ income ranks in each Census tract in the US. Following the differential privacy literature, we add noise to each regression estimate that is proportional to the sensitivity of the estimate, defined as the impact of changing a single observation on the statistic. Intuitively, if a statistic is very sensitive to a single observation, one needs to add more noise to keep the likelihood of disclosing a single person’s data below a given risk tolerance threshold.
The key technical challenge is determining the sensitivity of the regression estimates. The most common approach in the formal privacy literature is to measure the global sensitivity of the statistic by computing the maximum amount a regression estimate could change when a single observation is added or removed for any possible realisation of the data. The advantage of this approach is that the actual data are not used to compute sensitivity, permitting formal guarantees about the degree of privacy loss. The problem is that in practice, the global sensitivity of regression estimates is infinite – one can always formulate a dataset (intuitively, with sufficiently little variance in the independent variable) such that the addition of a single observation will change the estimate by an arbitrarily large amount. As a result, respecting global sensitivity effectively calls for adding an infinite amount of noise and hence does not provide a path forward to disclose standard OLS regression estimates.
At the other extreme, one can compute the local sensitivity of a regression statistic as the maximum amount a regression estimate changes when a single observation is added or removed from the actual data in a given sample. While this is a finite value, the problem with this approach is that releasing the local sensitivity of statistics may itself release confidential information. Intuitively, local sensitivity is itself a statistic computed in a small sample and thus reveals some information about the underlying data.
Our approach to computing sensitivity is a hybrid that lies between local and global sensitivity. We calculate local sensitivity in each cell (e.g. each Census tract) and then define the maximum observed sensitivity of the statistic as the maximum of the local sensitivities across all cells (e.g. across all tracts in a given state), adjusting for differences in the number of observations across cells. When one is interested in releasing an estimate for a single cell (e.g., a quasi-experimental estimate based on policy changes in a single school), one can construct ‘placebo’ estimates by pretending that similar changes occurred in other cells (other schools) and then following the same approach to compute the maximum observed sensitivity. Drawing on results from the differential privacy literature, we show that by adding noise proportional to the maximum observed sensitivity, one can guarantee that the privacy loss from releasing the cell-specific statistics (e.g., regression estimates) themselves falls below any desired exogenously specified risk tolerance threshold. Importantly, we can compute the maximum observed sensitivity in a sufficiently large sample that the disclosure risk from releasing it is likely to be negligible.
We then use our Opportunity Atlas application to demonstrate the benefits of these new methods relative to traditional approaches (focusing on count-based cell suppression), in terms of reducing both privacy loss and statistical bias. In terms of privacy loss, it is straightforward to show that cell suppression has infinite (uncontrolled) privacy risk. In contrast, our noise-infusion approach would yield only probabilistic information about the additional observation, with a probability that is controlled by the choice of the risk tolerance threshold. Our approach reduces the dimensionality of the statistics that create uncontrolled privacy risks to a single number (the maximum observed sensitivity parameter) that can be estimated in large samples, thereby significantly reducing the scope for privacy loss.
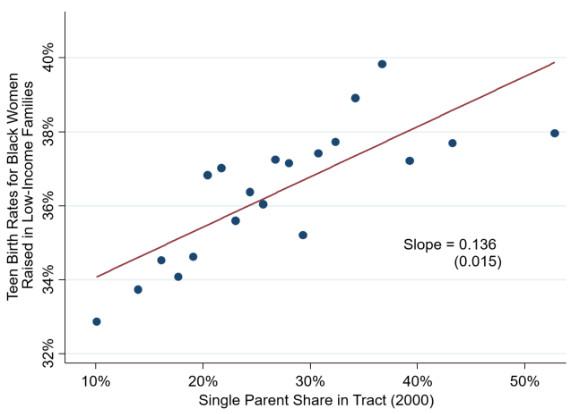
We demonstrate the benefits of our noise infusion approach in terms of statistical bias using an example from the Opportunity Atlas. Using noise-infused tract-level data, our prior work (Chetty et al. 2018) shows that black women who grow up in Census tracts with more single parents have significantly higher teenage birth rates. If one were to instead conduct their analysis suppressing cells where tracts where very few (less than five) teenage births occur – a common approach to limit disclosure risk for rare outcomes – this strong relationship would vanish and the correlation would be zero. Figure 1 below demonstrates the stark difference between this relationship in the true data, relative to that in the cell-suppressed data. This is because the suppression rule leads to non-random missing data by excluding cells with low teenage birth rates. In short, count suppression would have led us to entirely miss the relationship between teenage birth rates and single parent shares, illustrating how our algorithm outperforms existing approaches not just in principle but in practical applications of current interest to social scientists.
Figure 1 Association between teenage birth rates and single parent shares across Census tracts
A. Noise-infused data
B. Count-suppressed data
In summary, modern techniques from the differential privacy literature can provide a very useful approach for social scientists and government agencies seeking to release data based on small cells – one that minimises privacy risks while retaining the benefits of such data for scientific research and policymaking.
References
Angrist, J D, P A Pathak, and C R Walters (2013), “Explaining charter school effectiveness”, American Economic Journal: Applied Economics 5(4): 1–27.
Chetty, R and J N Friedman (2019), “A practical method to reduce privacy loss when disclosing statistics based on small samples”, American Economic Review Papers and Proceedings, forthcoming.
Chetty, R, J N Friedman, N Hendren, M R Jones and S Porter, “The Opportunity Atlas: Mapping the childhood roots of social mobility”, NBER Working Paper 25147,
Cooper, Z, S Craig, M Gaynor, and J Van Reenen (2015), “The price ain’t right? hospital prices and health spending on the privately insured”, NBER Working Paper No. 21815
Hull, P (2018), “Estimating hospital quality with quasi-experimental data”, working paper.