How important are external financial shocks for emerging market economies (EMEs)? What are the transmission channels of such shocks; and perhaps most importantly, what is the optimal monetary policy response to external financial shocks? This column aims to come up with possible answers to these policy relevant questions within the context of the Global Financial Crisis (GFC) event of the last decade.
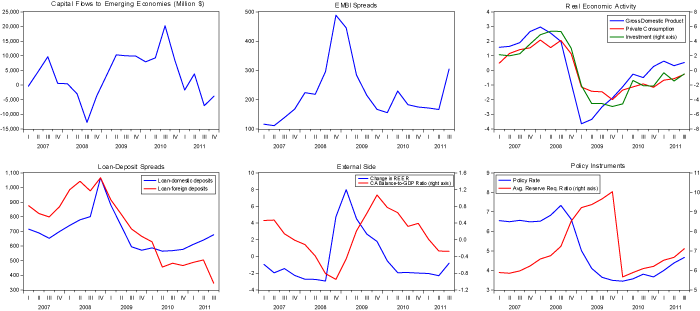
Although the GFC originated in advanced economies, its repercussions caused EMEs to suffer severe contractionary effects, identifying it as a large external adverse shock. We summarize major macro-financial developments in 20 EMEs around the 2007-09 episode in Figure 1.
Figure 1 Impact of Global Crisis in emerging markets, 2007—2009
Sources: BIS, Bloomberg, EPFR, IMF and individual country central banks.
Notes: Variables regarding real economic activity and the external side are depicted by cross-country simple means of deviations from HP trends. Medians of deviations produce similar patterns. Countries included: Brazil, Chile, China, Colombia, Czech Republic, Hungary, India, Indonesia, Israel, Korea, Malaysia, Mexico, Peru, Philippines, Poland, Russia, Singapore, South Africa, Thailand, and Turkey.
The top-left panel shows the sharp reversal of capital inflows to EMEs. This was accompanied by an increase of roughly 400 basis points in borrowing premiums as measured by the EMBI Global spread (the top-middle panel), coupled with sharp surges in lending spreads by around 400 basis points over the costs of domestic and foreign funds (the bottom-left panel).
Mihaljek (2011) also documented that the tightening in domestic financial conditions in EMEs coincided with substantial declines in domestic deposits and disproportionately more reduction in foreign debt of banks. This resulted in dramatic falls in bank loans to corporations.
Finally, the cyclical components of the real effective exchange rate and current account-to-GDP ratio (illustrated in the bottom-middle panel) highlighted a sharp depreciation and a reversal of about 10% and 2%, respectively. These adverse developments in domestic and external financial conditions paved the way to large drops in GDP and consumption (by around 4%) as well as in investment (by 8%) compared to their HP trend levels.
With the intention of mitigating the crisis, EME central banks first raised policy rates to curb accelerating capital outflows in the initial phase, and then gradually eased their policy stances (by about four percentage points in six quarters) thanks to the unprecedented monetary accommodation provided by advanced economy central banks in the aftermath of the crisis. This sensitivity of policy rates to global developments (including the reversals in the policy stance of advance economy central banks) revitalised the debate over whether central banks should pay attention to domestic or external financial variables beyond their effects on domestic inflation or real economic activity.
This debate is more appropriate in EMEs in which banks are the main source of credit extension. Furthermore, their sizeable reliance on noncore debt amplifies the transmission of external shocks, threatening both price and financial stability objectives.1
An example: although EME banks can deploy hedging instruments to cover FX borrowing risks, non-financial corporations have much limited access to such instruments, causing exchange rate risk on borrower firms to translate into credit risk for banks. Consequently, ‘lean against the wind’ (LATW) policies – defined as augmented Taylor-type monetary policy rules that additionally aim to achieve domestic or external financial stability – are now central to both academic and policy discussions about these non-trivial transmission channels of external risks (see Angelini 2011).
In our recent work (Mimir and Sunel 2015 and 2018), we provide a theory that replicates these features of the data. This allows us to explore the monetary policies that could be optimal from a welfare point of view. In particular, we study optimal monetary policy in an open economy with financial market imperfections with external shocks playing a central role.
First, we augment the canonical New-Keynesian DSGE model of a small open economy with a banking sector that has access to both domestic and foreign funding to construct the mechanisms through which external shocks spill over to the rest of the economy. We then investigate the quantitative performances of alternative optimal, simple and implementable LATW-type interest rate rules relative to a Ramsey-optimal monetary policy rule, following Schmitt-Grohe and Uribe (2007) to construct the rules. In particular, we explore the role of bank credit, asset prices, credit spreads, the US interest rate, and the real exchange rate as additional inputs to monetary policy. We then compare these optimal LATW-type Taylor rules with a standard optimised Taylor rule that would be responsive only to inflation and output gaps.
Optimal policy rules versus Ramsey-optimal policy
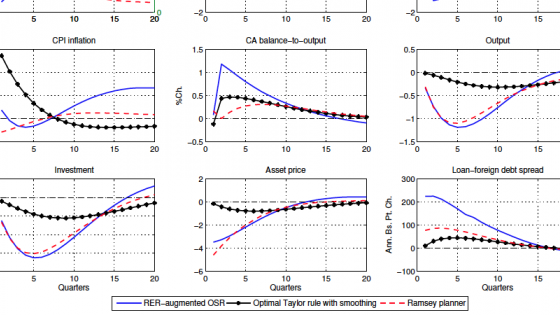
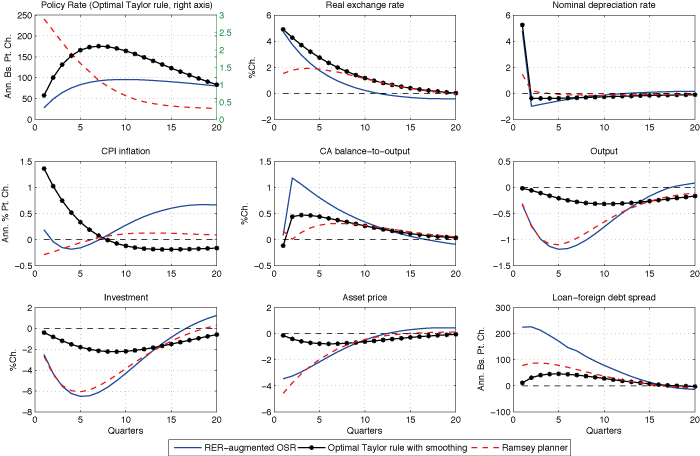
Figure 2 compares the impulses responses to a one standard deviation country risk premium shock under the Ramsey planner's economy (dashed plots) with selected optimal simple interest rate rules. In particular, we select the optimal real exchange rate-augmented interest rate rule (straight plots), since it produces the smallest welfare cost vis-à-vis the Ramsey-optimal policy and the optimal standard Taylor rule with smoothing (straight plots with asterisks) in order to highlight the departures of conventional wisdom from optimality in our setup. We highlight the country risk premium shock due to its strong explanatory power that emerges in the variance decomposition analysis.
Figure 2 Response of economy to risk premium shock under three policies
Source: Mimir and Sunel (2018).
The planner increases the policy rate by about 250 basis points per annum on impact in response to a 127 basis points annualised increase in the country borrowing premium. The sharp rise in interest rates mitigates capital outflows, enabling the planner to substantially reduce the reversal in the current account balance.
Both the nominal and real exchange rates depreciate only about 2%, which also contains the pass-through to CPI inflation via imported input goods. As a result, the annual CPI inflation rate falls a quarter of a percentage point on impact in the planner's economy, while it increases by 1 percentage point in the decentralised economy. The Ramsey planner also contains inefficient movements in the credit spreads over the cost of foreign debt and ensures that the credit spreads increase by less than 100 basis points in annualised terms. Notice that the second-best equilibrium warrants increased volatility in asset prices and investment compared to the decentralised economy. In that respect, the Ramsey planner trades off a smoother path for the real exchange rate and credit spreads against a more volatile trajectory for investment and output, to achieve a more stable path for the CPI inflation rate.
The optimal RER-augmented rule calls for an increase of 30 basis points in the policy rate in annualised terms under the country borrowing premium shock. This results in 3% more depreciation in the real exchange rate, and 1 percentage point higher increase in the inflation rate, compared to the Ramsey-optimal policy. As a result, credit spreads rise more, and there is a stronger reversal in the current account balance in comparison to the second-best economy. However, this optimised rule approximates the Ramsey-optimal policy fairly well in terms of bringing fluctuations in the asset price, investment and output closer to efficient fluctuations.[2]
Why does the model justify an emphasized response of domestic policy rates to the exchange rate? The answer hinges on three channels that are arguably important in an EME: the balance sheet channel, the trade channel, and the exchange rate pass-through. For the balance sheet channel, Kearns and Patel (2016) illustrated that depreciations have strong contractionary effects in EMEs, since balance sheet disruptions experienced by domestic borrowers may depress domestic demand. Therefore, the finance channel might offset the trade channel, which helps net exports to rise following large depreciations. On the other hand, there are well-understood inflationary effects of exchange rate depreciations that operate via pass-through from imported consumption and investment goods to home goods. Indeed, fluctuations in the exchange rate operate as endogenous cost-push shocks due to pass-through, which calls for optimal interest rate policy to aim exchange rate stability (Monacelli 2005 and 2013).
Comparing an optimised exchange rate-augmented interest rule with a standard Taylor rule underscores that it is not desirable to overlook exchange rate fluctuations in an EME. The optimal Taylor rule with interest rate smoothing (the lines with asterisks in Figure 2) displays only a mild response to inflation. It calls for a negligible rise (only 2 basis points per annum) in the short-term policy rate when the country risk premium shock hits the economy.
This finding resembles Aoki et al. (2016), in that in response to adverse external shocks (which already raise the cost of foreign debt) a strong anti-inflationary stance of interest rate policy would hurt bank balance sheets even more by increasing the cost of domestic deposits. This is precisely because this policy rule does not have any financial stabilisation objective to create space to fight inflation.
As a result, domestic currency is exchanged at about a 1% more depreciated level under this rule compared to that implied by the RER-augmented interest rate policy for 12 consecutive quarters. This in turn, results in a 1.4 percentage point rise in the CPI inflation rate on impact, due to the unmitigated exchange rate pass-through. Our quantitative welfare analysis suggests that although credit spreads, asset prices and investment are less volatile under this rule, the increased cumulative exchange rate depreciation, as well as the sharp rise in domestic inflation, means this policy rule is inferior to both the Ramsey-optimal policy and the RER-augmented interest rate policy.
Optimal policy rules compared to actual data
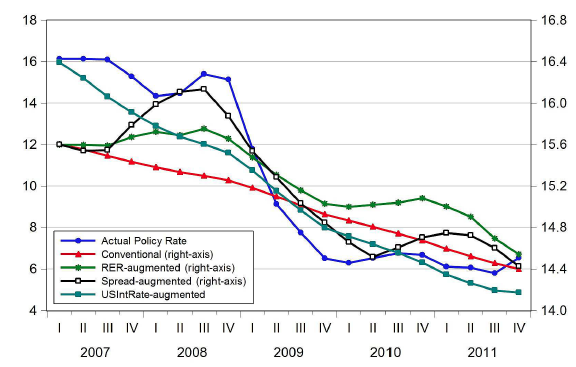
Figure 3 shows how the actual policy implementation of a representative EME central bank would fare with our alternative optimised interest policy specifications.
Figure 3 Comparison of rules for Central Bank of Turkey
Source: Mimir and Sunel (2018).
It compares trajectories for the optimal simple and implementable short-term policy rules with the empirical trajectory of the policy rate determined by a typical EME monetary authority, the Central Bank of the Republic of Turkey (CBRT). (Since the model is calibrated to the Turkish economy, we used the path of the key policy rate determined by the CBRT.)
To obtain the model implied trajectories, we feed the empirical time series for policy targets into the optimised, augmented Taylor rules. We find that a combination of the optimised US-interest-rate-augmented and credit-spread-augmented interest rate rules resembles the evolution of the actual policy rate in Turkey fairly well. The US-interest-rate-augmented rule captures the trend of the empirical series, while the credit-spread-augmented rule captures its cyclical properties.3 Note that the optimal standard Taylor rule does not capture either the absolute level, or the cyclicality of the empirical time series of the short term policy rate, successfully.
These findings suggest there could be a case for considering a wider spectrum of policy specifications in EMEs, especially when global conditions force policymakers in these countries to sail in uncharted waters. Our analysis, and the practice of EME central banks during and after the GFC, seem to confirm this insight.
Authors’ note: The views expressed in this paper are those of the authors only and do not necessarily reflect the views of Norges Bank or of the Bank for International Settlements (BIS). The usual disclaimer applies.
References
Angelini, P, S Neri, and F Panetta (2011), “Monetary and Macroprudential Policies,” Bank of Italy Economic working paper 801.
Aoki, K, G Benigno, and N Kiyotaki (2016), “Monetary and Financial Policies in Emerging Markets,” mimeo.
Ehlers, T and A Villar (2015), “The Role of Banks,” BIS Papers 83: 9–39.
Kearns, J and N Patel (2016), “Does the Financial Channel of Exchange Rates Offset the Trade Channel?”, BIS Quarterly Review.
Mihaljek, D (2011), “Domestic Bank Intermediation in Emerging Market Economies during the Crisis: Locally-owned versus Foreign-owned Banks”, BIS Papers 54: 31–48.
Mimir, Y and E Sunel (2015), “External Shocks, Banks and Optimal Monetary Policy in an Open Economy”, BIS working paper 528.
Mimir, Y and E Sunel (2018), “External Shocks, Banks and Optimal Monetary Policy: A Recipe for Emerging Market Central Banks,” International Journal of Central Banking, conditionally accepted for publication.
Monacelli, T (2005), “Monetary Policy in a Low Pass-Through Environment”, Journal of Money, Credit and Banking 37(6): 1047–1066.
Monacelli, T (2013), “Is Monetary Policy in an Open Economy Fundamentally Different?”, IMF Economic Review 61(1): 6–21.
Obstfeld, M (2015), “Trilemmas and Trade-offs: Living with Financial Globalisation”, BIS working paper 480.
Rey, H (2015), “Dilemma not Trilemma: The Global Financial Cycle and Monetary Policy Independence”, NBER working paper 21162.
Schmitt-Grohe, S and M Uribe (2007), “Optimal Simple and Implementable Monetary and Fiscal Rules”, Journal of Monetary Economics 54: 1702–1725.
Endnotes
[1] The median share of bank credit in total credit to the nonfinancial sector in EMEs was 87% in 2013 while the median share of noncore debt in total liabilities was 33%. For more details, see Ehlers and Villar (2015). For other related discussions, see Obstfeld (2015) and Rey (2015).
[2] Recall that the real exchange rate response coefficient of this rule hits its upper bound, suggesting that this policy could approximate the Ramsey-optimal policy even better if we allowed the response coefficient to take a larger value.
[3] The optimal credit-spread-augmented rule called for a negative interest rate response to a rise in loan-deposit rate differentials, which rise in bad times. The optimal US-interest-rate augmented rule, on the other hand, called for a positive response, to preserve an interest rate differential between EME and world interest rates, to avoid excess exchange rate depreciations.