Until a vaccine or cure defeats COIVD-19 by 21st century means, the best weapons we have are the ancient ones – quarantines, lockdowns, and the like. Yet all indications are that the current containment policies are too stringent to be tolerable for much longer in Europe and the US. Putting up with containment for a few weeks is one thing. Bearing them for many months is an entirely different thing.
Governments around the world are contemplating ways to ‘exit’ containment policies. Even if ‘exit’ is too optimistic of a word for what needs to happen, the necessity is clear. Governments face two fundamental, but conflicting imperatives, as Abele-Brehm et al. (2020) point out.
- The medical imperative (health constraint).
Social and professional interactions must be limited to avoid overloading the healthcare system and reduce the overall number of deaths. This could also be called the humanitarian constraint.
- The tolerance imperative (wealth constraint).
The population has limited acceptance of containment policies that disrupt economic, social, political, and even religious aspects of their lives. This could also be called the societal constraint.
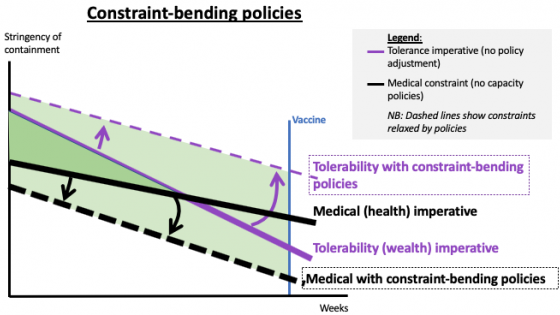
Many analysts approach the problem as it if were a standard, Econ101 trade-off. They think of it as a ‘dollars versus deaths’ trade-off, or more politely a balancing between the economy and the people. In my last VoxEU column, I proposed an alternative perspective based on constrained optimisation, and a diagram for thinking schematically about solutions. Figure 1 shows the basic infographic.
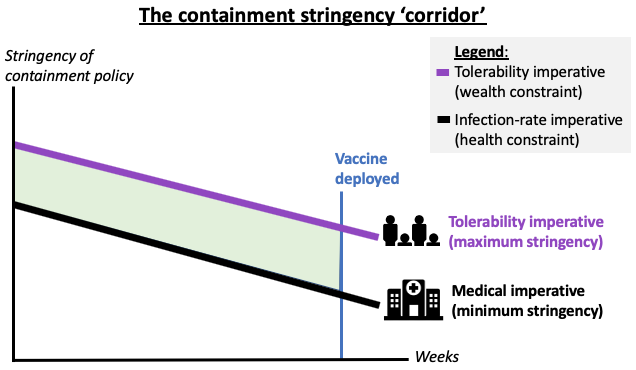
The stringency corridor diagram
The vertical axis shows the stringency of containment policies. This reflects the severity of the restrictions we are all experiencing in the name of ‘World War COVID’. The horizontal axis shows time. The problem ends once a vaccine is widely available, so this endpoint is shown with the blue vertical line.
Figure 1 The ‘containment stringency corridor’
Source: Author’s elaboration. Lines are drawn as linear for drafting convenience.
The heavy black line illustrates the minimum stringency that is necessary to satisfy the medical imperative. It’s downward sloping for at least two reasons.
- As hospital capacities expand over time, the system can handle more patients.
In terms of stringency, higher hospital capacities mean that supportable infection rates are higher, and thus the necessary stringency is lower.
- As time passes, the fraction of the population that is susceptible to infection falls since people who have had it become immune (I assume it is lasting).
The disease administers a ‘natural’ (but very dangerous) vaccine to a growing share of the population. This is the famous ‘herd immunity’ that Britain and Sweden strove for. Practically, it means the health constraint can be satisfied at a lower level of stringency.
The tolerance imperative (heavy purple line) defines the maximum stringency that people can put up with. In the illustration it is drawn as falling over time. Again, there are two reasons for this.
- People gradually get fed up with social sacrifices.
The constraint, however, is not just about boredom and yearnings.
- Not working means not producing and that, in turn, means lower consumption.
When stocks and inventories run low, as they will (and already have for some items), keeping a large fraction of the workforce away from work means the population will have to cut their consumption by an equally large fraction. Eventually, it means shortages, higher prices, and perhaps rationing and material hardships for vulnerable citizens, as I pointed out in my VoxEU column four weeks ago (Baldwin 2020c).
Money can help shield financially vulnerable people but, in aggregate, extra spending does no good if there are no goods to buy. This is a key economic reason why the population’s acceptance of any given level of stringency will diminish over time. And it is why boosting tolerance of continued containment policies requires workforce remobilisation.
Money can help shield financially vulnerable people but, in aggregate, extra spending does no good if there are no goods to buy. This is a key economic reason why … boosting tolerance … requires workforce remobilisation.
Before employing the ‘stringency corridor’ diagram to think about strategies, it is worth asking: What is meant by stringency?
Stringency measured
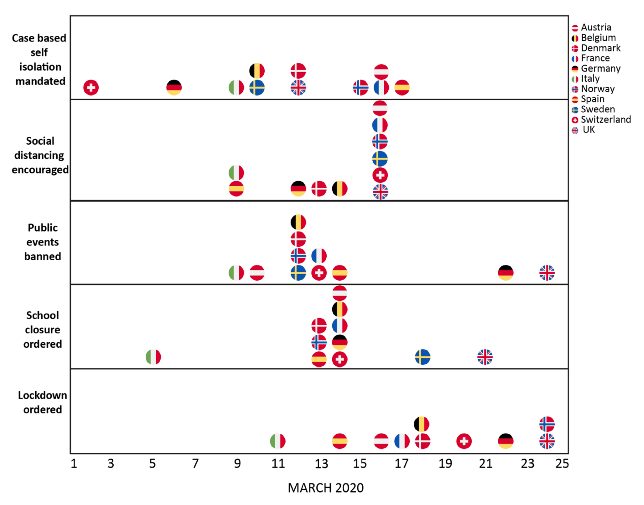
Flaxman et al. (2020) provide a useful categorisation of containment policies (being scientists, they call them ‘non-pharmacological interventions’) and they provide data on when European nations adopted them (Figure 2). Roughly speaking, the stringency increases for the policies further down the chart.
Figure 2 One typology of containment policies and dates of adoption.
Source: Flaxman et al (2020), Figure 1.
Notes: The least stringent policy is case-based self-isolation mandated (e.g. a 14-day self-quarantine period for people returning from outbreak areas), social distancing recommended (working from home, maintaining two-metre distances from others, etc.), public events banned (this was often done progressively with first large events cancelled, going all the way to all gatherings banned), university and school closures, and finally lockdowns (this itself ranges in strictness among nations and cities).
Thinking back on past failures
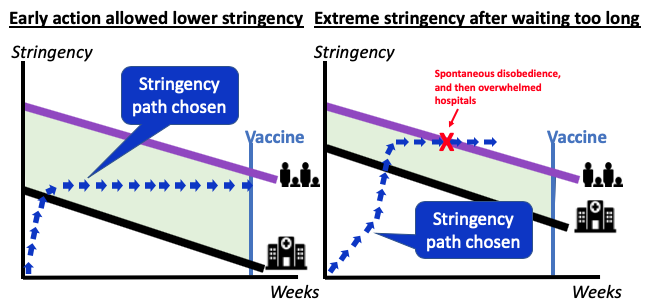
The corridor diagram is useful for illustrating the contrasting outcomes in countries, like Denmark, which embraced measured containment policies early on, and those like Britain which waited too long and were forced to adopt extreme containment measures.
The left panel of Figure 3 illustrates how early action allow the medical constraint to be met with less stringent policies (epidemiological simulations show this to be the case – e.g. Ferguson et al. 2020). The lower medical constraint (heavy black line) means that the nation can ‘win’ the war with a less stringent containment policy.
The right panel shows a hypothetical where the nation waits will the disease is well into its accelerating phase – a phase where the number of cases can double in two days or less. Delay at this point has cruel implications. Hospitals are overwhelmed, or doctors raise the alarm that they are soon to be overloaded. At this point, governments have reacted by imposing extreme restrictions and enforcing them via security services or even the military. Since the restrictions are so acute, they are hard to maintain for long without running into the tolerance barrier. This is schematically shown in the right panel.
Figure 3 Thinking about good and bad stringency strategies: Early versus too late
Source: Author’s elaboration.
Thinking ahead on exit/remobilisation strategies
It’s becoming increasingly clear that the world will not ‘exit’ the current containment policies until a vaccine is ready, but the workforce must be remobilised, at least in part. The ‘corridor diagram’ suggests a straightforward way of organising thinking about exiting from today’s severest restraints.
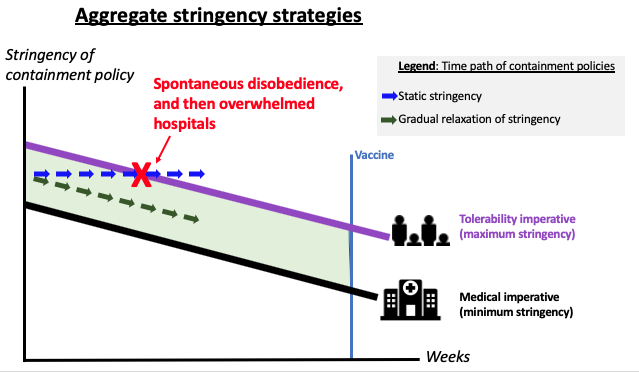
Figure 4 illustrates the challenges. The current level of stringency is schematically depicted with the blue arrows. The problem is that if the containment policies remain at current levels, the tolerability imperative will be violated. That means people will ignore them. Depending on circumstances, the verb ‘ignoring’ could mean anything from sly and peaceful violations to public and violent upheavals (Baldwin 2020c).
There is a stringency path that gets the nation from today to the vaccine point without overwhelming hospitals or overwhelming citizens’ stamina. The strategy, however, requires some thinking ahead. It requires an adaptive, progressive relaxation of the containment policy stringency. Figure 4 illustrates the point.
There is a stringency path that gets the nation from today to the vaccine point without overwhelming hospitals or overwhelming citizens’ stamina. The strategy, however, requires some thinking ahead. It requires an adaptive, progressive relaxation of the containment policy stringency. Figure 4 illustrates the point.
Many governments are planning such relaxations. As the Financial Times reported on 5 April 2020, “France, Spain, Belgium and Finland are among many countries that have set up expert committees to examine a gradual easing of stay-at-home orders for some businesses and schools while avoiding a second wave of infections that could overwhelm health services” (Hall 2020).
Figure 4 Static versus adaptive stringency strategies
Source: Author’s elaboration. Lines are drawn as linear for drafting convenience.
In the underlying assumptions behind Figures 1, 3 and 4 are fundamentally optimistic. There is always a way to ‘win World War COVID’. There is a stringency path that threads its way between the health and wealth imperatives.
When there is no easy answer
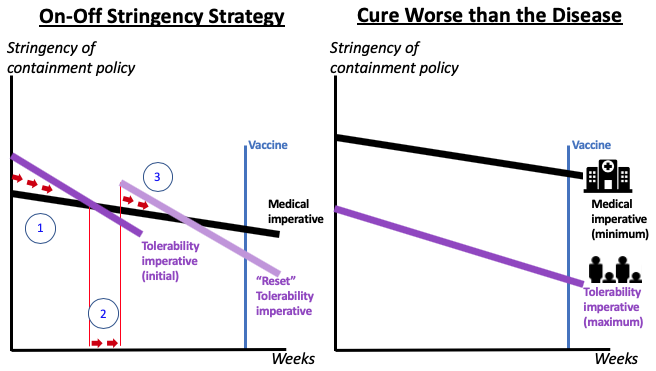
This is not the only possibility. It is not inevitable that a problem with two constraints can be solved. In terms of the ‘corridor diagram’, it is possible that the green path narrows to nothing, so no stringency strategy works. Figure 5 (left panel) shows one such situation.
In the left panel, lockdowns and shutdowns can work for a while, but the stringency path (red arrows) eventually ends up violating one or both imperatives. A possible solution, which seems to be one that some governments are actively considering, is an intermittent containment strategy.
It is not inevitable that a problem with two constraints can be solved. In terms of the ‘corridor diagram’, it is possible that the green path narrows to nothing, so no stringency strategy works. Figure 5 (left panel) shows one such situation.
Ferguson et al. (2020), for instance, simulate the outcome of an explicit solution of the type that is called ‘bang-bang’ in optimal control theory, or ‘little-s, big-S’ or ‘(s, S)’ in inventory management. Their proposal is for the UK to turn on strict containment when 100 intensive care unit (ICU) cases are observed in a week. When ICU cases fall to 50 per week, social distancing and school and university closures are removed. All other containment policies remain in force throughout. Under their simulations of the disease’s progress, strict containment would have to be in place for two-thirds of the time from now till the autumn of 2021.
Figure 5 Examples of more difficult scenarios
Source: Author’s elaboration. Lines are drawn as linear for drafting convenience.
The implicit reasoning behind this plan is that removing the most economically onerous restrictions intermittently would in some sense ‘reset’ the population’s tolerance for further restrictions. In the left panel this is shown as a broken path marked by the red arrows. There are three phases as illustrated (this assumes, for drafting convenience, total relaxation in phase 2). Further phases (not shown) would be needed in this example.
Allowing intermittent remobilisation of workers would surely help boost production, but there are many issues to be considered such as difficulties in resuming production quickly. On the social tolerance side, the feasibility is really a matter for social psychologists. What the corridor diagram contributes is a clarification of what the policy is meant to accomplish. It would shift just one of the two constraints. On the economic side, allowing workers to work would relieve some the supply shortages that are likely to appear, and help some businesses avoid bankruptcy.
The right panel of Figure 5 illustrates a far more heartrending scenario … the minimum medical constraint is everywhere above the tolerability constraint … we might think of this as the situation facing emerging and developing nations. These nations do not have the fiscal capacity to launch massive spending packages that help people tolerate lockdowns.
The right panel of Figure 5 illustrates a far more heartrending scenario. Here, the minimum medical constraint is everywhere above the tolerability constraint. There is, in this version, no solution that respects both constraints. Since one of the things that has rendered containment policies bearable are the massive spending policies announced by North Atlantic economies, we might think of this as the situation facing emerging and developing nations. These nations do not have the fiscal capacity to launch massive spending packages that help people tolerate lockdowns, work closures, travel restrictions and the like. These packages are hugely costly.
Advanced economy governments are implementing spending packages that are on par with wartime spending. Neta Crawford, a professor of political science at Boston University, estimates that the Iraq war cost the US about $2 trillion (Crawford 2020). The US Congress has already approved a phase 1 package that large to help make the effects of containment policies economically tolerable (and shield firms, jobs, and banks from permanent damage). Few emerging markets can afford this. And without income support and protection for small firms, restaurants and the like, people cannot respect containment policies without risking hunger or worse. Likewise, disrupting supply chains when a large fraction of the population is close to subsistence and has no financial reserves may just not be possible.
What is the solution? The first best would be to mobilise international help – as suggested, for example, by UNCTAD (2020). Failing that, the disease will run its course until the nation builds up so-called ‘herd immunity’. This is something like a very costly way of administering a vaccine. People actually have to contract and survive the disease to acquire immunity. If a high enough fraction of the population is immune, transmission of the disease can fall off dramatically, according to simulations by epidemiologists.
Bending the constraints – support, remobilisation, etc.
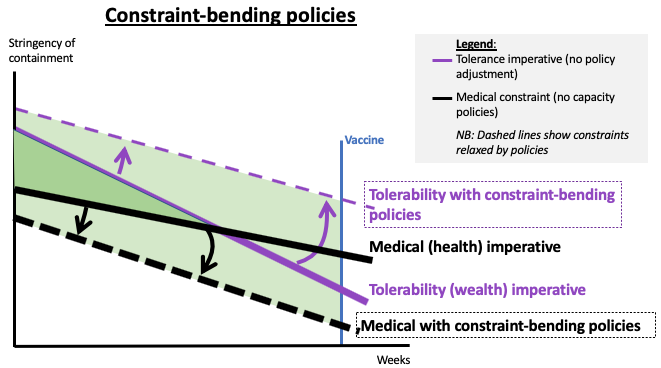
Analysts simplify to clarify because the world is so complex. Trying to account for everything leaves you with an understanding of nothing. One simplification that comes with the ‘corridor analysis’ is a clear separation of measures that ‘bend’ the medical imperative and those that bend the tolerability imperative. One that bends both constraints in the right direction is testing. But before addressing testing, consider an indicative list of measures that bends the tolerability constraint.
Figure 6 Corridor-widening policies on the health and on the wealth sides
Source: Author’s elaboration. Lines are drawn as linear for drafting convenience.
On the tolerance side, there are really two types of measures: those that allow a greater resumption of economic activity for any given level of stringency, and those that make people feel better about containment policies.
- As mentioned, the greatest of all are the compensation or shielding packages that are often mislabelled as ‘stimulus’ packages.
These are sheltering firms, banks, and productive networks from permanent damage. In Europe, they have also sought to pay for essential consumption for society’s most vulnerable members. Without this help from governments, it is unlikely that so many Europeans would be sitting at home today. In the US, for instance, gig-economy workers, and workers without formal contracts are continuing to work since they have to work to survive (Liu 2020).
In terms of the corridor diagram, the government packages can be thought of as shifting the heavy black line up – since any stringency level is more acceptable – and rotates it counter clockwise – since peoples’ patience wears thin less quickly when they know, for example, that they still have a job.
- The second most important tolerance-bending actions are those related to remobilisation.
Most of the remobilisation plans discussed by economists can be thought of as increasing the population’s ability to live with containment. Here I’m thinking of plans like Boeri et al. (2020), Schnetzer et al. (2020), and Abele-Brehm et al. (2020); many more are in the pipeline.
Here’s the point. To get more economic production from the same level of aggregate stringency, governments could vary the restrictions – by age of workers, by state of health, by occupation, or by location. Since production in modern economies often involves complex networks, governments could get more production from the same number of workers by coordinating better – say, among suppliers and producers, and logistic providers.
The battle against COVID-19 is war, and as in wars, the issue is not the dollar-cost of reducing casualties. The issue is how society can achieve the medical imperative without overstretching citizens’ tolerance. The key is to, on one hand, pursue policies that increase the medical effectiveness of any given level of stringency, and, on the other hand, pursue policies that make any given level of stringency more tolerable.
Along the social psychology angle, there are many policies that make confinement more tolerable – things like the ‘circuses’ part of Juvenal’s famous ‘more bread and circuses’. I’ll leave these aspects for qualified professionals, but one thing that seems clear from my experience of teaching from confinement is that the banning of all public meetings is harsh. For instance, moving back to allowing small groups of people to meet (with proper distancing and personal protection precautions) would assuage some of the tension that has built up. Exams could be held and subjects that require laboratory work could proceed. Medical constraints can also be relaxed.
Policies that relax the medical constraint – in the sense that the same infection rate can be achieve with less-stringent containment policies – include things like getting basic medical information before the eyes of more people. Things like simple personal hygiene measures (hand washing and disinfection) are powerful tools but not everyone knows about them (or has them front-of-mind). Here are some other actions that can reduce the chance of infection at any given level of social interaction and thus relax the medical constraint.
- Using masks and gloves.
- Rearranging retail shops, workplaces and school setting to reduce social interaction.
- Encouraging online shopping.
- Adopting smart phone-based tracking apps that reduce the chances of infectious people coming in contact with susceptible people.
Testing as the cure-all
Testing is the ultimate silver bullet in keeping the corridor open. As Dewatripont et al. (2020) put it: “restarting economic activity as quickly as possible is crucial but … requires the reliable identification of individuals who will not contract the virus or transmit it to others.”
The US and European nations have had to rely on extreme containment policies since they do not know who is infectious and who is susceptible. Things are different in some East Asian nations. As I wrote in my VoxEU column three weeks ago, Singapore used testing and contact-tracing to separate the sick from the susceptible. The policy “involved rapid response, extensive testing, and isolation of infected people and people they might have given it to. The key to all of that was testing. Singapore was able to determine who was infected” (Baldwin 2020e). This meant they could keep sick and healthy apart without having to keep everyone apart (as Europe and the US have had to do).
With widespread testing, nations could allow back into the workforce only those workers who can neither get it nor give it. By restoring consumption, this would make any aggregate level of containment more tolerable.
Concluding remarks
Governments around the world face heart-wrenching choices. Strict containment policies will reduce COVID’s death toll, but keeping them in effect until the vaccine appears is untenable. This column suggests that the standard economic approach to this trade-off is a mischaracterisation. This is not a situation where calculating ‘dollars versus deaths’ trade-offs will be helpful.
The battle against COVID-19 is war, and as in wars, the issue is not the dollar-cost of reducing casualties. The issue is how society can achieve the medical imperative without overstretching citizens’ tolerance. The key is, on one hand, to pursue policies that increase the medical effectiveness of any given level of stringency and, on the other hand, to pursue policies that make any given level of stringency more tolerable.
References
Abele-Brehm, A et al. (2020), “Making the Fight against the Coronavirus Pandemic Sustainable,” Group of German Scientists, coordinated by Clemens Fuest and Martin Lohse, 2 April.
Baldwin, R and B Weder di Mauro (eds) (2020a), Economics in the Time of COVID-19, a VoxEU.org eBook, CEPR Press.
Baldwin, R and B Weder di Mauro (eds) (2020b), Mitigating the COVID economic crisis: Act fast and do whatever it takes, a VoxEU.org eBook, CEPR Press.
Baldwin, Richard (2020a). “It’s not exponential: An economist’s view of the epidemiological curve,” VoxEU.org, 12 March 2020.
Baldwin, R (2020b). “Inequality and pandemic make an explosive mix,” VoxEU.org, 15 March.
Baldwin, R (2020c). “The supply side matters: Guns versus butter, COVID-style,” VoxEU.org, 22 March.
Baldwin, R (2020d). “COVID, remobilisation and the ‘stringency possibility corridor’”, VoxEU.org, 10 April.
Baldwin, R (2020e). "Testing for testing times,” VoxEU.org, 26 March.
Boeri, T, A Caiumi and M Paccagnella (2020). “Mitigating the work-security trade-off,” VoxEU, 09 April.
Correia, S, S Luck, and E Verner (2020). “Pandemics Depress the Economy, Public Health Interventions Do Not: Evidence from the 1918 Flu.” Mimeo.
Crawford, N (2020). “The Iraq War has cost the US nearly $2 trillion,” The Conversation, 4 February.
Eunjung Cha, A, L Bernstein, F Stead Sellers and S Harris (2020), “Faced with a crush of patients, besieged NYC hospitals struggle with life-or-death decisions,” Washington Post, 1 April.
Ferguson, N M, D Laydon, G Nefjati-Gelani et al. (2020), “Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand”, Imperial College COVID-19 Response Team.
Flaxman, S et al. (2020). “Report 13 - Estimating the number of infections and the impact of non-pharmaceutical interventions on COVID-19 in 11 European countries,” MRC Centre for Global Infectious Disease Analysis, Imperial College COVID-19 Response Team.
Gollier, C and S Straub (2020), “Some micro/macro insights on the economics of coronavirus. Part 2: Health policy,“ VoxEU.org, 03 April.
Gourinchas, P-O (2020), “Flattening the pandemic and recession curves,” Chapter 2 in R Baldwin and B Weder di Mauro (eds), Mitigating the COVID economic crisis: Act fast and do whatever it takes, a VoxEU.org eBook, CEPR Press.
Hall, B and G Chazan (2020), “Europe prepares to ease coronavirus lockdowns,” Financial Times, 5 April.
Liu, J (2020). “‘I simply won’t be able to meet my day-to-day living expenses:’ How coronavirus is impacting gig workers,” 24 March 2020, CNBC.com.
Sanche S, Y T Lin, C Xu, E Romero-Severson, N Hengartner and R (2020), “High contagiousness and rapid spread of severe acute respiratory syndrome coronavirus 2”, Emerg Infect Dis. 26(7).
Schnetzer, M, D Tamesberger and S Theurl (2020), “Mitigating mass layoffs in the COVID-19 crisis: The Austrian short-time model”, VoxEU.org, 07 April.
UNCTAD (2020). “UN calls for $2.5 trillion coronavirus crisis package for developing countries,” 30 March.
US Office of Defense Mobilization (1951), Report to the President by the Director of Defense Mobilization, Washington, DC.
WHO (2020), Report of the WHO-China Joint Mission on Coronavirus Disease 2019 (COVID-19), February.