Did medieval pogroms prefigure Nazi zealotry? Does the slave trade continue to affect trust between people in Africa? Does a country’s prosperity depend on the genetic diversity of its population? Do arbitrary colonial boundaries continue to drive poverty in Peru and internal conflict in Africa?1
These and other questions are part of a substantial literature on persistence, or deep origins, which finds that many modern outcomes strongly reflect the characteristics of the same place in the more or less distant past.
Naturally, any such findings are open to the usual complaints about p hacking, about answers in search of questions, about simplistic explanations of complex phenomena, and so on. But all of these objections crumble into irrelevance in the face of one blunt fact –the unusual explanatory power of these persistence variables.
While a judicious choice of variables or time periods might coax a t statistic towards 1.96, there would seem to be no way that the t statistics of four, five, or even higher that appear routinely in this literature could be the result of massaging regressions, no matter how assiduously. There is no arguing with a significance level of 0.0001. Such persistence results must instead reflect the deep structural characteristics that drive historical processes – the enduring legacies of the past.
However, alongside unusually high t statistics, persistence regressions usually display extreme levels of spatial autocorrelation of residuals. In a well-behaved regression, residuals should show no pattern, whereas in persistence studies neighbouring places tend to have similar values of residuals – high beside high, and low beside low. This raises the question of whether the unusual explanatory power of some persistence regressions might be a consequence of fitting spatial noise, reflected in the spatial pattern of their residuals.
To investigate this, in a recent paper (Kelly 2019) I begin by simply carrying out synthetic regressions of one spatial noise variable on another, and find that t statistics become seriously inflated, even when the correlation between places disappears quite rapidly with distance.
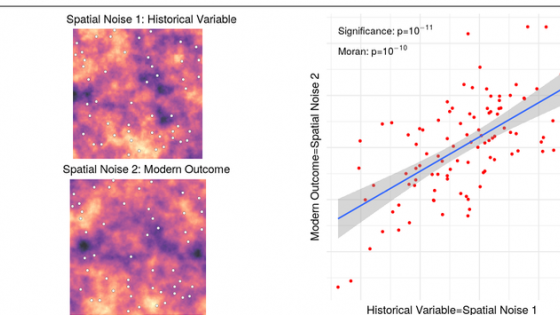
Figure 1 A regression of one spatial noise variable on another can appear highly significant
Figure 1 gives the basic idea. I generate two spatial noise series – where areas with high values are coloured yellow and those with low values purple – and take their values at the white dots which correspond to towns. I will call one noise series the ‘modern’ outcome (say, GDP per capita or attitudes toward immigrants), and the other I label the ‘historical’ variable (say, deaths in the Thirty Years’ War or duration of rule by the Ottoman Empire).
If you regressed one variable on the other without knowing that they are both artificial noise, you would probably conclude from Figure 1 that the ‘historical’ variable exerts an overwhelming impact on the ‘modern’ outcome. However, even if we are not told that the variables are spatial noise, there turns out to be a reliable indicator to caution us that our findings may be specious, and that indicator is the Moran statistic. The Moran statistic is the standard test for spatial autocorrelation in regression residuals, and extreme values such as those in Figure 1 act as a warning that there might be a lot less to our regression results than we would hope. No study that I examine below reports Moran statistics.
Statistics is about extracting structure from data. The difficulty with spatial noise patterns, as the coloured simulations in Figure 1 illustrate, is that they contain a lot of apparent order, like faces in clouds. This structure makes it perilously easy to unearth spurious patterns and mistake them for convincing evidence of deep historical processes.
With this in mind, I analyse the results of 28 persistence papers that have appeared in the American Economic Review, Econometrica, Journal of Political Economy, and Quarterly Journal of Economics to assess their robustness to spatial noise. The approach is to replicate the first substantive regression of the paper using spatial noise first as an explanatory variable, and then as the dependent variable.
I am only interested in the robustness of these studies to spatial noise, and not in any issues of data reliability, regression specification or the quality of their historical scholarship (although in most cases this is extremely high). Above all, and this cannot be emphasised too strongly, I am not interested in the findings of any particular study – least of all to somehow validate or ‘disprove’ them – except insofar as they illustrate the broader contours of the literature. The fact that the first regression in a paper is problematic does not imply that the later ones, which typically include more control variables, are equally so.
Figure 2 The Moran statistic indicates that most persistence regressions exhibit severe spatial autocorrelation of residuals
The Z scores of Moran statistics for each regression are shown in Figure 2 and we can see that, with some exceptions, the spatial autocorrelation in these results is extreme.
The next step is to replace regression variables with artificial noise, in two ways. First, I replace the explanatory, persistence variable with spatial noise to see how their predictive power compares. Then I switch things around and use noise as the dependent variable, to see how well the persistence variable can explain what it should not be able to explain.
Figure 3 Persistence variables with high nominal significance frequently have less explanatory power than spatial noise
Figure 3 shows the nominal significance level of the persistence variable, along with the fraction of times that spatial noise outperforms it in terms of explanatory power. To handle the extreme significance levels of many studies, the figure uses a logarithmic axis truncated at 10-9. We can see that the studies with low Moran statistics are rarely outperformed by noise. At the other end are some persistence variables that appear to have significance levels of one in a million but are beaten by noise over one third of the time.
Figure 4 Many persistence regressions can strongly predict spatial noise
Turning to Figure 4, this shows how often the persistence variable can explain spatial noise with a significance level of 0.001 or 0.0001. It can be seen here that some studies with low Moran statistics do quite well at explaining noise, but this simply highlights the importance of that statistic – in all of those simulations the Moran statistic is high, reflecting the fact that they are constructed to be noise regressions.
The findings here show that it is easy to fit regressions to spatial noise that appear to have impressive explanatory power. Fortunately, however, we have seen that this trap is easily avoided by generating spatial noise and using it to replace the explanatory and dependent variables in succession.
More straightforwardly still, we have seen that a standard Moran statistic serves as a useful warning light for potential trouble with spatial noise. My results suggest that in cases where this statistic is not reported the findings of persistence studies (and regressions using spatial data more generally) should be treated with some caution.
References
Acemoglu, D, S Johnson and J A Robinson (2001), “The colonial origins of comparative development: An empirical investigation”, American Economic Review 95: 1369-1401.
Acemoglu, D, S Johnson and J A Robinson (2002), “Reversal of fortune: Geography and institutions in the making of the modern world income distribution”, Quarterly Journal of Economics 117: 1231-1294.
Acemoglu, D, T A Hassan and J A Robinson (2011), “Social structure and development: A legacy of the Holocaust in Russia”, Quarterly Journal of Economics 126: 895-946.
Alesina, A, P Giuliano and N Nunn (2013), “On the origin of gender roles: Women and the plough”, Quarterly Journal of Economics 128: 469-530.
Alsan, M (2015), “The effect of the tsetse fly on African development”, American Economic Review 105: 382-410.
Ashraf, Q and O Galor (2011), “Dynamics and stagnation in the Malthusian epoch”, American Economic Review 101: 2003-2041.
Ashraf, Q and O Galor (2013), “The “out of Africa” hypothesis, human genetic diversity, and comparative economic development”, American Economic Review 103: 1-46.
Banerjee, A and L Iyer (2005), “History, institutions, and economic performance: The legacy of colonial land tenure systems in India”, American Economic Review 95: 1190-1213.
Becker, S O. and L Woessmann (2009), “Was Weber wrong? A human capital theory of Protestant economic history”, Quarterly Journal of Economics 24: 531-596.
Becker, S O and L Pascali (2019), “Religion, division of labor and conflict: Anti-Semitism in German regions over 600 Years”, American Economic Review 109: 1764-1804.
Dell, M (2010), “The persistent effects of Peru’s mining mita”, Econometrica 78: 1863-1903.
Durante, R, P Pinotti and A Tesei (2019), “The political legacy of entertainment TV”, American Economic Review 109: 2497-2530.
Galor, O and Ö Özak (2016), “The agricultural origins of time preference”, American Economic Review 106: 3064-3103.
Hornung, E (2014), “Immigration and the diffusion of technology: The Huguenot diaspora in Prussia”, American Economic Review 104: 84-122.
Juhász, R (2018) “Temporary protection and technology Adoption: Evidence from the Napoleonic blockade”, American Economic Review 108: 3339-3376.
LaPorta, R, F Lopez de Silanes, A Shleifer and Robert W Vishny (1998), “Law and finance”, Journal of Political Economy 106: 1113-1155.
Kelly, M (2019), “The standard errors of persistence”, CEPR discussion paper 13783.
Michalopoulos, S (2012), “The origins of ethnolinguistic diversity”, American Economic Review 102: 1508-1539.
Michalopoulos, S and E Papaioannou (2013), “Pre-colonial ethnic institutions and contemporary African development”, Econometrica 81: 113-152.
Michalopoulos, S and E Papaioannou (2016), “The long-run effects of the scramble for Africa”, American Economic Review 106: 1802-1848.
Nunn, N (2008), “The long-term effects of Africa’s slave trades”, Quarterly Journal of Economics 123: 139-176.
Nunn, N and N Qian (2011), “The potato’s contribution to population and urbanization: Evidence from a historical experiment”, Quarterly Journal of Economics 126: 593-650.
Nunn, N and L Wantchekon (2011), “The slave trade and the origins of mistrust in Africa”, American Economic Review 101: 3221-3252.
Putterman, L and D N Weil (2010), “Post 1500 population flows and the long-run determinants of economic growth and inequality”, Quarterly Journal of Economics 125: 1627-1682.
Satyanath, S, N Voigtländer and H-J Voth (2017), “Bowling for fascism: Social capital and the rise of the Nazi party”, Journal of Political Economy 125: 478-526.
Spolaore, E and R Wacziarg (2009), “The diffusion of development”, Quarterly Journal of Economics 124: 469-529.
Squicciarini, M and N Voigtländer (2015), “Human capital and industrialization: Evidence from the age of enlightenment”, Quarterly Journal of Economics 30: 1825-1883.
Valencia Caicedo, F (2019), “The mission: Human capital transmission, economic persistence, and culture in South America”, Quarterly Journal of Economics 134: 507-556.
Voigtländer, N and H-J Voth (2012), “Persecution perpetuated: The medieval origins of anti-Semitic violence in Nazi Germany”, Quarterly Journal of Economics 127: 1339-1392.
Endnotes
[1] See Voigtländer and Voth (2012) on medieval pogroms and Nazi zealotry, Nunn and Wantchekon (2011) on the slave trade and trust between people in Africa today, Ashraf and Galor (2013) on prosperity and genetic diversity, and Dell (2010) and Michalopoulos and Papaioannou (2016) on colonial boundaries and poverty in Peru and conflict in Africa, respectively.