European integration was, from its origins, a project of peace, shaped by the destruction and suffering brought by the two World Wars. Economic integration, it was believed, would lead to increased economic interdependence and better understanding, both generated by trade flows. The objective was to make conflict unthinkable, and judged from this point of view it has been a great success. The European experience seems therefore to prove Kant and Montesquieu right. Both philosophers held the view that trade between nations is a pacifying force as illustrated by this quote from Montesquieu (1758): “The natural effect of trade is to bring about peace. Two nations which trade together render themselves reciprocally dependent.” Outside Europe, this vision of trade as an engine of peace has also been very influential: MERCOSUR was created in 1991 in part to curtail the military power in Argentina and Brazil, then two recent and fragile democracies with ongoing disputes over natural resources and borders. These disputes are still present but have not escalated into military conflicts, which can, at least partly, be interpreted as a consequence of MERCOSUR. After the end of the Cold War, some commentators went further and interpreted the forces of globalisation as putting an end to centuries of inter-state conflicts, some going to the point of predicting “the end of history”. If indeed, trade between countries promotes peace, as suggested by the European example, then it seems logical that the dramatic increase of trade flows at the global level should lower the number of violent interstate conflicts.
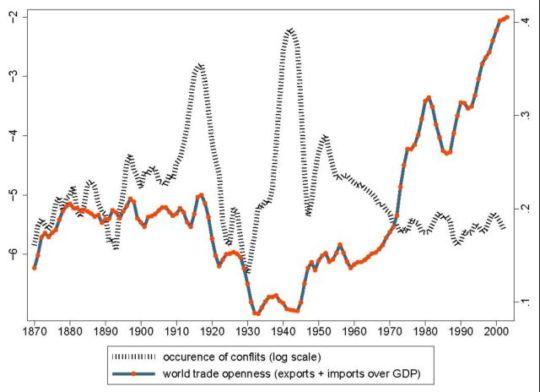
So what went wrong? Why is it that globalisation, interpreted as trade liberalisation at the global level, has not lived up to its promise of decreasing the prevalence of violent interstate conflicts? Since 1970, the occurrence of military inter-state conflicts has remained constant, whereas global trade as a percentage of world GDP has more than doubled. Looking at a larger time span, figure 1 suggests that during the 1870-2001 period, the relation between trade openness (the ratio of trade to GDP at the world level) and war is nothing but simple.1 The first era of globalisation, at the end of the 19th century, was a period of rising trade openness and of multiple military conflicts, culminating with World War I. Then, the interwar period was characterised by a simultaneous collapse of world trade and of conflicts. After World War II, world trade increased rapidly while the number of conflicts decreased (although the risk of a global conflict was obviously high). But again, since 1970 trade flows increased dramatically, but there is no evidence of a lower prevalence of military conflicts – even taking into account the increase in the number of sovereign states.
To go further, we have tried to understand the reason why the logic of pacifying trade seems to work at the bilateral or regional level but cannot be simply extended at the global level.2 Our conclusion, based on extensive empirical work using a large dataset of military conflicts on the 1950-2000 period, and taking into account many other possible determinants of conflicts, is that the intuition that trade is good for peace is only partially true. The part that is true is that two countries that trade more bilaterally indeed have a lower probability of a bilateral conflict. The intuition is that bilateral trade generates economic gains that are put into danger if a dispute between two countries escalates into a military conflict. We indeed check that the destruction of bilateral trade following bilateral conflicts is large and persists for twenty years. Hence, higher bilateral trade flows are a measure of the opportunity cost of such a conflict and create an incentive to accept concessions to avoid military escalation.
However, it is wrong to take the seemingly logical next step and conclude that globalisation leads to more peaceful relations between countries. In fact, we find that countries that are more open to trade with the rest of the world are more inclined to military conflicts. Another way to put it is that two countries that trade more with each other pacify their bilateral relations but make it more likely that a conflict will arise with a third country. The interpretation of this seemingly provocative result is that when two countries are very open to trade, the bilateral economic dependence and therefore the opportunity cost of a bilateral conflict are lowered. The incentive to make concessions in order to avert escalation is weakened when globalisation provides economic insurance during bilateral conflicts by diversifying trade partners.
Globalisation is by construction an increase in both bilateral and multilateral trade flows. What then was the net effect of increased trade since 1970? We find that it generated an increase in the probability of a bilateral conflict by around 20% for those countries separated by less than 1000kms, the group of countries for which the risk of disputes that can escalate militarily is the highest. The effects are much smaller for countries which are more distant.
Contrary to what these results (aggravated by our nationality) may suggest, we are not anti-globalisation activists even though we are aware that some implications of our work could be (mis)used in such a way. The result that bilateral trade is pacifying brings several more optimistic implications on globalisation. First, if we think of a world war as a war between two large groups or coalitions of countries, then globalisation makes such a war less likely because it increases the opportunity cost of such a conflict. Obviously, this conclusion cannot be tested but is a logical implication of our results. From this point of view, our work suggests that globalisation may be at the origin of a change in the nature of conflicts, less global and more local. Second, our results do confirm that increased trade flows created by regional trade agreements (such as the EU) are indeed pacifying as intended. Given that most military conflicts are local, because they find their origins in border or ethnic disputes, this is not a small achievement. These beneficial political aspects of regional trade agreements are not usually considered by economists who often focus on the economic distortions brought by their discriminatory nature. Given the huge human and economic costs of wars, this political effect of regional trade agreements should not be discounted.
This opens interesting questions on how far these regional trade agreements should extend – a topical issue in the case of the EU. The entry of Turkey in the EU would indeed pacify its relations with EU countries (especially Greece and Cyprus), but also increase the probability of a conflict between Turkey and its non-EU neighbours. However, our simulations suggest that in this case, the first effect dominates the second by a large margin.
More generally, our results should be interpreted as a word of caution on some political aspects of globalisation. As it proceeds and weakens the economic ties of proximate countries, those with the highest risk of disputes that can escalate into military conflicts, local conflicts may become more prevalent. Even if they may not appear optimal on purely economic grounds, regional and bilateral trade agreements, by strengthening local economic ties, may therefore be a necessary political counterbalance to economic globalisation.
Footnotes
1. More precisely, the number of country pairs which in a given year are in a military conflict divided by the number of existing country pairs.
2. For details, see Make Trade not War?