The press often reports stories of smuggling and other forms of evasion of border taxes. For instance, in April 2018 Chinese customs detained 17 people in their operation targeting “a smuggling crime syndicate” which had illegally imported $98.4m worth of salmon from Norway (Kynge 2018). In 2014, Pakistani customs uncovered a scam involving over 100 containers of cloth that were cleared at less than half of the usual duty rate (Express Tribune 2014). Even the UK experiences “a continued smuggling problem around cigarettes and alcohol” (Houlder 2017).
Evasion of border taxes, just like tax evasion in general, is difficult to detect because parties involved have every incentive to conceal their illegal behaviour. In a recent paper, we propose using Benford’s Law, which describes the distribution of first digits in economic or accounting data, as a tool in the fight against evasion (Demir and Javorcik 2018).
Benford’s Law
Benford’s Law describes the distribution of first (leading) digits in economic or accounting data. It is based on the empirical observation that, contrary to what one might expect, the leading digits in various types of numerical data are not uniformly distributed – the occurrence of the digits 1 to 9 as, for instance, the first leading digit is not equally likely. Instead, the probability of the occurrence of the digits 1 to 9 monotonically decreases – the digit 1 appears as the first leading decimal digit on average 30% of the time, while the digit 9 appears 4.6% of the time (see Figure 1).
Figure 1 Benford’s distribution of first digits
Notes: The figure shows the distribution of the leading first digits as predicted by Benford’s Law, Prob (First digit is d) = log10(1 + 1/d).
The law naturally arises when data are generated by an exponential process or independent processes are pooled together. So far, deviations from Benford’s distribution have been used to detect reporting irregularities in macroeconomic data (Michalski and Stoltz 2013) and in survey data (Judge and Schechter 2009).
Data manipulated for the purpose of evasion are likely to display significant deviations from Benford’s Law. It is because, as shown by experimental research, people do a poor job of replicating known data-generating processes, by, for instance, over-supplying modes or under-supplying long runs (Camerer 2003: 134-38). Moreover, since Benford’s Law is not widely known, it seems very unlikely that those manipulating numbers would seek to preserve fit to the Benford distribution.
Should Benford’s Law hold in import data?
One can expect Benford’s Law to hold in international trade data for three reasons. First, ‘second-generation’ distributions – that is, combinations of other distributions, such as, quantity multiplied by price (as in trade transaction values) conform with Benford’s Law (Hill 1995). Second, Benford’s Law holds for right-skewed distributions – that is, distributions where the mean is greater than the median (Durtschi et al. 2004), which is a characteristic of import values.
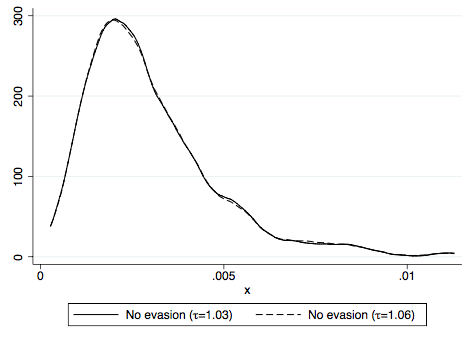
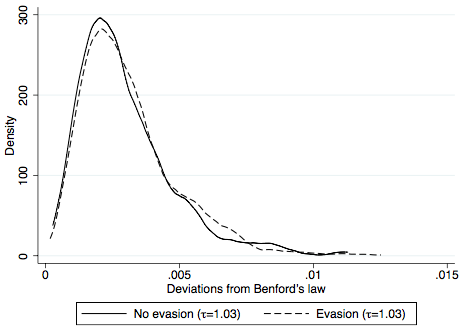
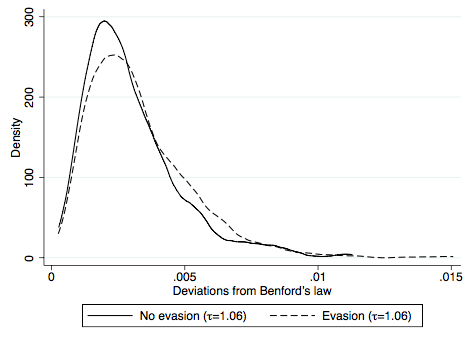
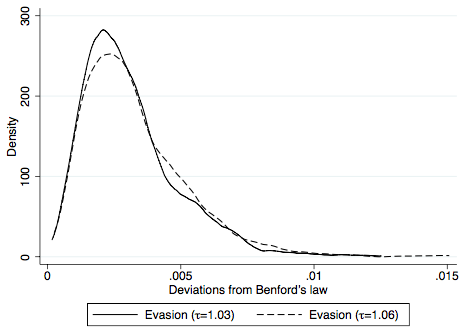
Third, a simulation exercise shows that trade values generated by a standard international trade model comply with Benford’s Law in the absence of tax evasion and that evasion leads to significant deviations from the law. The simulation exercise considers four scenarios: no evasion with a low tax rate (3%), no evasion with high tax rate (6%), evasion with low tax rate (3%), and evasion with high tax rate (6%). Deviations from Benford’s Law are calculated as the sum of squared differences between the observed and predicted frequency of first digits over 1–9. As illustrated in Figure 2, the average deviation is significantly higher with evasion than in the benchmark case without evasion. In the presence of evasion, an increase in the tax rate is also associated with larger deviations from the law.
Figure 2 Deviations from Benford’s Law in simulated data
Notes: These figures show deviations from Benford’s Law in simulated data for trade values based on a standard Armington-type trade model. See Demir and Javorcik (2018) for details.
Application to Turkish imports data
We use Benford’s Law to examine evasion in the aftermath of an unexpected policy change in Turkey. On 13 October 2011, the Resource Utilisation Support Fund (RUSF) tax, which applies to imports utilising external financing, increased from 3% to 6% of the transaction value.
We employ detailed imports data, disaggregated by the exporting firm, product, source country, month–year, and financing terms for the period October 2009 to September 2012. Exposure to the tax is measured as the share of imports coming with external financing at the product-source country level (hereafter referred to as variety level) before the policy change. Then we examine whether deviations from Benford’s Law within a product-country cell increase after the policy change with the initial exposure to the tax.
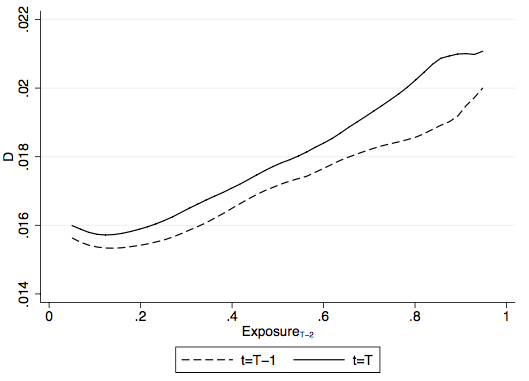
Figure 3 confirms that this is indeed the case. It shows that deviations from Benford’s Law are positively associated with the exposure of varieties both 12 months before and 12 months after the policy change. However, the gap between the two lines is wider at higher levels of exposure. This result is consistent with higher tax evasion after the RUSF rate doubled in October 2011. It is further confirmed by a formal econometric exercise. This conclusion is also confirmed using a well-established approach based on discrepancies in international trade statistics, as proposed by Fisman and Wei (2004).
Figure 3 Deviations from Benford’s Law and exposure
Notes: The figure shows local polynomial regressions of Turkish imports reported by the source country and Turkey as functions of Exposure, which is defined as the share of imports with external financing at time t = T – 2 (24-months before the policy change at t=T).
Source: Demir and Javorcik (2018).
Conclusion
Our study has practical implications. It suggests that Benford’s Law could be used by authorities to decide where to channel resources in their fight against tax evasion. A simple test showing a positive relationship between deviations from Benford’s Law and the applicable tax/tariff rate would be quite suggestive of evasion taking place and would call for further scrutiny. Such a test could be applied to import flows using a particular mode of transport, crossing a particular checkpoint, or even being cleared by a particular customs officer. The test could be performed using import transaction data that are collected by customs and hence readily available.
References
Camerer, C (2003), Behavioral Game Theory: Experiments in Strategic Interaction, New Age International.
Demir, B and B Javorcik (2018), “Forensics, elasticities and Benford's Law: Detecting tax fraud in international trade,” CEPR Discussion Paper 12798.
Durtschi, C, W Hillison and C Pacini (2004), “Effective use of Benford’s Law to assist in detecting fraud in accounting data,” Journal of Forensic Accounting 4.
Express Tribune (2014), “Tariff evasion: Customs seize dry port records to probe Rs170 million scam,” Express Tribune, 5 December.
Fisman, R and S-J Wei (2004), “Tax rates and tax evasion: Evidence from missing imports in China,” Journal of Political Economy 112(2): 471–500.
Hill, T P (1995), “A statistical derivation of the significant-digit law detecting problems in survey data using Benford’s Law,” Statistical Science 4.
Houlder, V (2017), “UK tax fraud unit recovers £5.2bn in a year,” Financial Times, 30 October.
Judge, G and L Schechter (2009), “Detecting problems in survey data using Benford’s Law,” Journal of Human Resources 44(1).
Kynge, J (2018), “China-focused salmon smuggling ‘syndicate’ spawns raids,” Financial Times, 12 April.
Michalski, T and G Stoltz (2013), “Do countries falsify economic data strategically? Some evidence that they might,” Review of Economics and Statistics 95(2): 591–616.