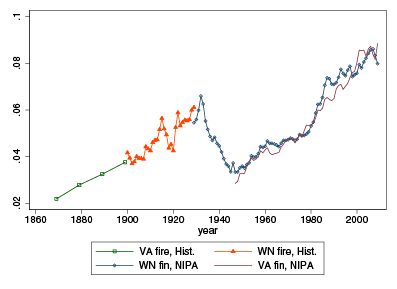
The role of the finance industry is to produce, trade, and settle financial contracts that can be used to pool funds, share risks, transfer resources, produce information, and provide incentives. Financial intermediaries are compensated for providing these services.
Measuring financial intermediation
The sum of all profits and wages paid to financial intermediaries represents the cost of financial intermediation. I measure this cost from 1870 to 2010, as a share of GDP, and find large historical variations, shown in Figure 1 (with the various data sources, see Philippon 2011 for details). The cost of intermediation grows from 2% to 6% from 1870 to 1930. It shrinks to less than 4% in 1950, grows slowly to 5% in 1980, and then increases rapidly to almost 9% in 2010. The pattern remains the same if finance is measured as a share of services, and if net financial exports are excluded.
Figure 1. The GDP share of the finance industry
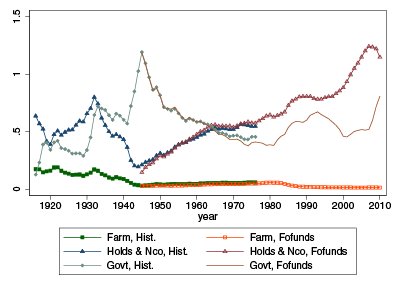
Then comes the issue of measuring the output of the financial sector. I show in Philippon (2011) that a simple benchmark can be constructed using the workhorse of modern macroeconomics, a neoclassical growth model. This benchmark is a weighted average of the financial assets created by the financial sector for the real economy. For instance, for the debt market, we must look at bonds issued by farms, households and non-profit organisations, and the government (Figure 2).
Figure 2. A few debt Markets
For the corporate sector, we need to look at bonds and stocks, and for stocks, we want to distinguish seasoned offerings and IPOs. We also need to look at the liquidity benefits of deposits and money market funds. When we put all the pieces together, we obtain a series for output for the finance industry. (For a discussion of how to account for financial derivatives, see Philippon 2011).
The decreasing efficiency of intermediation in the US
We can then estimate the cost of financial intermediation, defined as the value-added share divided by output series. The cost of intermediation in the US is between 1.3% and 2.3% over 130 years. However, the finance cost index has been trending upward, especially since the 1970s. This is counter-intuitive. If anything, the technological development of the past 40 years – in IT in particular – should have disproportionately increased efficiency in the finance industry. How is it possible for today's finance industry not to be significantly more efficient than the finance industry of John Pierpont Morgan?
It is important to understand that the neoclassical benchmark that I am using assumes that all agents borrow rationally ex ante (of course, that does not rule out the fact that they might end up with too much debt ex post, but that means that they understand the risks involved and choose to borrow). We can debate this assumption, but the point I want to emphasise is that this provides an upper bound on financial efficiency. If anything, adding excessive risk taking and over-borrowing would decrease the risk-adjusted efficiency (for an insightful discussion, see Haldane and Madouros 2011, Popov and Smets 2011, and Arcand et al. 2011, all on this site).
Information technologies: Where is Wal-Mart when we need it?
An obvious driving force in financial intermediation is information technology. I often hear the argument that improvements in IT explain the increase in the share of finance. This argument, however, is either incomplete or misleading. One reason it is incomplete is simply that IT cannot explain the evolution of the GDP share of finance before 1970.
What makes the IT argument misleading is that it is far from clear why IT should increase the share of finance. The neoclassical growth model predicts that, in most cases, technological improvement should lower the share of GDP spent on financial intermediation. In particular, this prediction is unambiguous for most retail finance. Essentially, the physical transaction costs of buying and holding financial assets must have decreased because of IT. This effect must have lowered the amount spent on intermediation.
Figure 3. IT investment and size in retail and wholesale trade
An apt analogy is with retail and wholesale trade. After all, these are also intermediation services. There is a clear analogy between retail banking and retail trade. As Blanchard (2003) explains in his discussion of Basu et al. (2003), “fully one-third of the increase in TFP growth from the first to the second half of the 1990s in the United States came from the retail trade sector. For this reason, the general merchandising segment, which represents 20% of sales in the sector, was one of the sectors examined in a McKinsey study (McKinsey Global Institute 2001) aimed at understanding the factors behind US TFP growth in the 1990s.” Figures 3a and 3b show the evolution of GDP shares and IT investment in wholesale trade, retail trade, and Figure 4 shows this evolution for finance.
Figure 4. IT investment and size in finance
The contrast is striking. Based on what we see in wholesale and retail trade, IT should have made finance smaller, not larger.
What happened? Why did we get the bloated finance industry of today instead of the lean and efficient Wal-Mart? Finance has obviously benefited from the IT revolution and this has certainly lowered the cost of retail finance. Yet, even accounting for all the financial assets created in the US, the cost of intermediation appears to have increased. So why is the non-financial sector transferring so much income to the financial sector?
One simple answer is that technological improvements in finance have mostly been used to increase secondary market activities, i.e., trading.
Figure 5. Equity trading volume over GDP
Figure 5 shows the dollar volume of equity trading over GDP in the US. The finance industry of 1900 was just as able as the finance industry of 2000 to produce bonds and stocks, and it was certainly doing it more cheaply. But the recent levels of trading activities are at least three times larger than at any time in previous history. Trading costs have decreased (Hasbrouck 2009), but the costs of active fund management are large. French (2008) estimates that investors spend 0.67% of asset value trying (in vain, by definition) to beat the market.
I conclude that the most important questions in finance today are:
- A positive question: Why do people (fund mangers, households, etc.) trade so much?
- A normative question: Has increased trading led to either better prices or better risk sharing?
I would like to believe that the answer to (ii) is yes, but I am still waiting for the evidence. If the answer turns out to be no, then we would have to conclude that the finance industry's share of GDP is about 2 percentage points higher than it needs to be and this would represent an annual misallocation of resources of about $280 billion for the US alone.
References
Arcand, J-L, E Berkes, U Panizza (2011), "Too much Finance?", VoxEU.org, 7 April.
Basu, S, JG Fernald, N Oulton, and S Srinivasan (2003), “The Case of the Missing Productivity Growth”, in M Gertler and K Rogoff (eds.), NBER Macroeconomics Annual.
Blanchard, O (2003), “Comment on Basu et al.”, in M Gertler and K Rogoff (eds.), NBER Macroeconomics Annual.
Bolton, P, T Santos, and J Scheinkman (2011), “Cream Skimming in Financial Markets”, Working Paper, Columbia University.
French, KR (2008), “Presidential Address: The Cost of Active Investing”, The Journal of Finance, 63(4):1537-1573.
Haldane, AG and V Madouros (2011), "What is the Contribution of the Financial Sector, VoxEU.org, 22 November.
Hasbrouck, J (2009), “Trading Costs and Returns for U.S. Equities: Estimating Effective Costs from Daily Data”, Journal of Finance, 64(3):1445–1477.
McKinsey Global Institute (2001), "US productivity growth 1995-2000. Understanding the Contribution of Information Technology Relative to other Factors”, Washington, D.C.
Philippon, T (2011), “Has the US Finance Industry Become Less Efficient?”, mimeo NYU.
Popov, A and F Smets (2011), “On the tradeoff between growth and stability: The role of financial markets”, VoxEU.org, 3 November.