In social interactions, what determines cooperative behaviour, or enables us to act in ways that are beneficial not only to us, but to our neighbours, people in the same country or who share the same planet? What induces us to do more than just say "I care’’, but act in ways that make others better off as well as ourselves?
In other words, what makes us effective social animals?
Economists and other social scientists have provided many explanations. Cooperation may originate from warm feelings, and consideration of others can motivate us towards generous and cooperative behaviour. According to this argument, a cohesive society is one where good, generous feelings inspire our actions (Dawes and Thaler 1988, Isaac and Walker 1988, Fehr and Gaechter 2000, Fehr and Schmidt 1999, Falk et al. 2008, among others).
Another suggestion is that good norms and institutions provide a blueprint for socially useful behaviour. According to this interpretation, a harmonious society is built on good norms and trust consistently followed (Putman 1994, Coleman 1988, among others) or on institutions inherited from the past that work well (Acemoglu et al. 2001, among others).
A final possibility is that insightful self-interest guides us to become good citizens. According to this suggestion, cooperation arises in society when people are smart enough to foresee the social consequences of their actions, including the consequences for others.
In recent work (Proto et al., forthcoming), we test these three possible suggestions experimentally. We find overwhelming support for the idea that intelligence is the primary condition for a socially cohesive, cooperative society. Warm feelings and good norms have an effect too, but it is transitory and small.
Good heart, good norms, and intelligence
Our experiments are based on games. A game is a set of rules that assigns a payoff to two people depending on what both choose to do. Repeating the game several times, meaning that the two players know that they will meet again, allows each player to react to what the other one has done in the previous periods.
The repetitions in our study have a random termination, with a frequency controlled by the experimenter. A higher continuation probability represents a more lasting social interaction. These repeated games are non-zero-sum games. In other words, there is room for cooperative – mutually beneficial – behaviour, but also for selfish, mutually damaging behaviour. This is an essential feature because it reflects the interactions we experience most frequently in real life.
We then create two 'cities', or groups of subjects. The two groups differ according to one of the three characteristics: good heart, good norms, or intelligence. We pay particular attention to the frequency with which they chose cooperative behaviour, called the cooperation rate.
We study several games. We consider first the prisoners’ dilemma. When this is played as a one-shot game, defecting (not cooperating with the other player) gives a higher payoff, whatever the other chooses. But if the game is infinitely repeated, cooperative action can become optimal for each individual, producing an equilibrium where both players cooperate in every period, because of the threat of reverting to the defecting equilibrium after a deviation. Note that, at this equilibrium, there is a trade-off between the current payoff (larger if a player defects) and long-run payoff (smaller if the player defects).
Intelligence
We measure intelligence using the subjects' performance in the Raven progressive matrices test. When we create groups in which subjects in one group have higher intelligence than those in the other, we observe that the higher intelligence group learns to work together, achieving almost full cooperation. In the group of less intelligent subjects, the cooperation rate declines from the initial level (Figure 1).
Figure 1 Cooperation rates of high- and low-intelligence groups of subjects when playing a random termination, repeated prisoners’ dilemma
Note: Players assigned to groups using results of Raven progressive matrices test.
Good heart
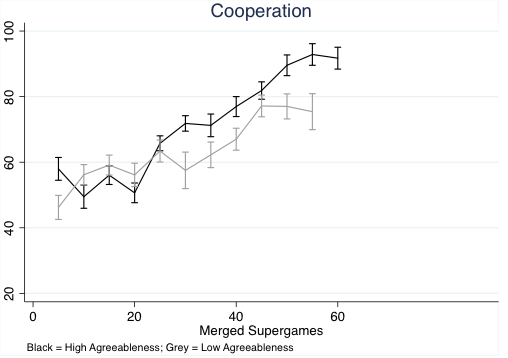
We next create two groups according to their level of agreeableness, a ‘Big 5’ personality trait which measured levels of positive social inclinations (trust and generosity). Figure 2 shows the cooperation rates of these two groups when they play an infinitely repeated prisoners’ dilemma. Cooperation rates in the two agreeableness groups are not clearly different.
Figure 2 Cooperation rates among high- and low-agreeableness groups of subjects when playing a random termination, repeated prisoners’ dilemma
Note: Players assigned to groups using results of a Big 5 personality questionnaire.
Good norms
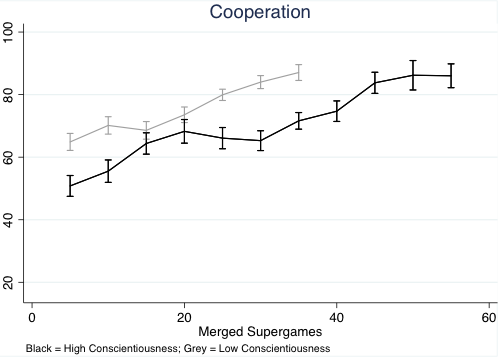
Finally, we create groups distinguished by their level of adherence of social norms. We identify this by conscientiousness, defined as the tendency to be organised and dependable, show self-discipline and dutifulness. Conscientiousness is also one of the Big 5 traits. Figure 3 shows the cooperation rates among the two groups of subjects. We find that, rather than cooperating more, the high-conscientiousness group learns to cooperate more slowly than the low-conscientiousness group. This result suggests that higher levels of compliance with social norms do not guarantee higher levels of cooperation. Our analysis suggests that this occurred because highly conscientious subjects were too cautious in their choices. This delayed convergence to full cooperation.
Figure 3 Cooperation rates among high- and low-conscientiousness groups of subjects when playing a random termination, repeated prisoners’ dilemma
Note: Players assigned to groups using results of a Big 5 personality questionnaire.
The effect of intelligence in simpler games
To gain more insight on the way intelligence affects cooperation, or learning to cooperate, we asked the two intelligence groups to play simpler games, which have no trade-off between current payoff and long-run payoff. The stag hunt game is one example, in which players must decide whether to hunt a stag or a hare. Hunting a stag yields a higher payoff if the other player also hunts a stag, but a low payoff if the other player hunts a hare. Hunting a hare yields an intermediate but sure payoff, whatever the other player decides to do.
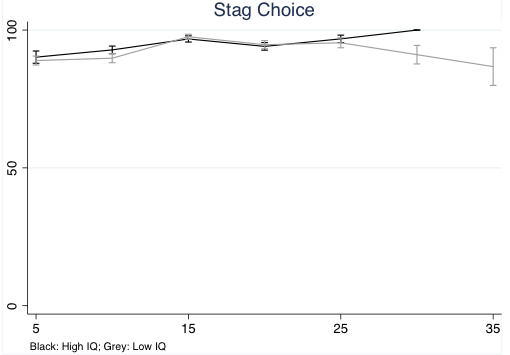
If players meet once only, it is optimal to hunt a stag only if the player expects that the other player will do the same. But when this game is repeated, once both players manage to coordinate in hunting a stag, they have nothing to gain in either the short or the long run from deciding to hunt a hare instead. Figure 4 shows the coordination rates for hunting a stag – there is no substantial difference between high- and low-intelligence groups. Both groups quickly learn to co-ordinate on hunting a stag, and do not change their behaviour afterwards. Battle of the sexes, another game with no trade-off between short-run and long-run payoffs, gives the same result.
Figure 4 Co-ordination rates to hunt stag of high-IQ and low-IQ groups of subjects playing indefinitely repeated Stag Hunt game in different laboratory sessions
Note: Players assigned to groups using results of Raven progressive matrices test.
Goal neglect
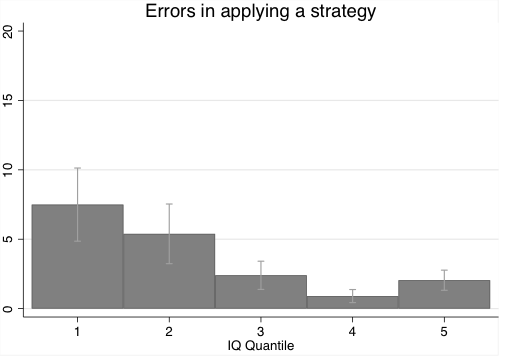
Our hypothesis is that in games without a trade-off between short-run and long-run payoffs, the effect of intelligence on cooperation is smaller. This is a similar effect to the goal neglect in non-strategic choices of lower-intelligence individuals demonstrated by Duncan et al. (2008). In this study, the authors experimentally showed that more intelligent people tended to apply previously chosen strategies more consistently. In our experiments, when individuals played a game in which short-term objectives conflicted with long-term ones, they would occasionally neglect their long-term goal and to make payoff-reducing errors. Figure 6, shows the errors committed by subjects, split by quantile of intelligence. Lower quantiles made more errors.
Figure 5 Errors in applying a strategy by subjects in the repeated prisoners' dilemma game, by quantile of IQ distribution
Note: 'Error' defined as defection when, in previous period, subjects cooperated.
References
Acemoglu, D, S Johnson and J A Robinson (2001), “The colonial origins of comparative development: An empirical investigation”, American Economic Review 91(5): 1369-1401.
Coleman, J S (1988), "Social Capital in the Creation of Human Capital", American Journal of Sociology 94: S95-S120.
Dawes, R M and R Thaler (1988), ‘‘Cooperation’’, Journal of Economic Perspectives II: 187–197.
Duncan, J, A Parr, A Woolgar, R Thompson, P Bright, S Cox, S Bishop, and I Nimmo-Smith (2008), "Goal neglect and Spearman's g: competing parts of a complex task", Journal of Experimental Psychology: General 137(1): 131-148.
Falk, A, E Fehr, U Fischbacher (2008), "Testing theories of fairness—Intentions matter", Games and Economic Behaviour 62(1): 287-303.
Fehr, E and K Schmidt (1999), "A theory of fairness, competition, and cooperation", Quarterly Journal of Economics 114: 817–868.
Fehr, E and S Gaechter (2000), "Cooperation and Punishment in Public Goods Experiments", American Economic Review 90(4): 980–994.
Isaac, M R and J M Walker (1988), ‘‘Group Size Effects in Public Goods Provision: The Voluntary Contribution Mechanism’’, Quarterly Journal of Economics 103(1): 179–199.
Proto, E, A Rustichini, A Sofianos (forthcoming), "Intelligence, Personality and Gains from Cooperation in Repeated Interactions", Journal of Political Economy.
Putnam, R D (1994), Making Democracy Work: Civic Traditions in Modern Italy, Princeton University Press.