The slope of the yield curve, also known as the term spread (TMS) of interest rates, has long been of interest to policymakers and financial market participants alike. Despite being a good in-sample predictor of the equity risk premium (Chen et al.1986, Campbell 1987, Fama and French 1989), it performs rather poorly out-of-sample (e.g.Goyal and Welch 2008).
In a recent paper, we use wavelet filtering methods to extract economically motivated frequency components from the US TMS and then study their role for predicting the equity risk premium (ERP) out-of-sample in the US equity market (Faria and Verona 2018). In particular, we isolate the high-frequency component of the TMS (which captures fluctuations between 2 and 16 months), the business-cycle-frequency component (which captures cycles between 16 and 128 months), and the low-frequency component of the TMS (which captures fluctuations with a period exceeding 128 months).
We find that the low-frequency component of the TMS (TMS-LF hereafter) is a strong and robust out-of-sample ERP predictor, both in the short run (one month-ahead) and in the long run (two years ahead). In contrast, the high-frequency and business cycle-frequency components of the TMS are rather poor ERP predictors.
This finding adds to recent empirical evidence (e.g.Dew-Becker and Giglio 2016) showing that the level and price of aggregate risk in equity markets are strongly linked to low-frequency economic fluctuations, supporting time-varying expected returns and return predictability. From a theoretical point of view, as pointed out for example by Rapach and Zhou (2013), return predictability is also compatible with market efficiency. In fact, asset returns depend on the state of the real economy, which is characterised by significant business-cycle fluctuations. So, if the quantity and price of aggregate risk are linked to economic fluctuations, then one should expect time-varying returns and return predictability, even if markets are efficient.
Data and methodology
The term spread is computed as the difference between the US 10-year government bond yield and the 3-month Treasury bill. The equity risk premium is computed as the difference between the S&P500 index total return and the one-month Treasury bill.
We use monthly observations from January 1973 to December 2017. The out-of-sample forecasts are produced using a sequence of expanding windows. We use an initial sample (January 1973 to December 1989) to make the first out-of-sample forecast. The sample is then increased by one observation and a new out-of-sample forecast is produced. We repeat this procedure until the end of the sample. The out-of-sample evaluation period is thus from January 1990 to December 2017.
Why is the TMS-LF a good predictor of the equity risk premium?
A standard way to test the economic value of the TMS-LF’s predictive ability is to form a trading strategy for a mean-variance investor that allocates his or her wealth between equities and risk-free bills and uses the equity risk premium forecast from the TMS-LF. In our analysis, we limit the exposure to the equity market to -50% and 150%, therefore limiting the possibilities of short-selling and leveraging the portfolio.
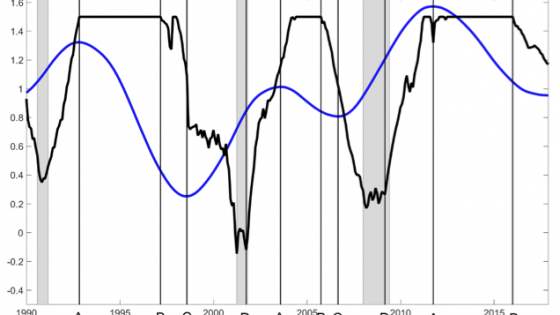
The economic mechanism underlying our empirical results can be summarised as follows. An increase in the TMS-LF predicts high equity returns, because it predicts low discount rates. This implies an increased appetite for risk-taking, triggering an increased future equity exposure.1 This lead-lag pattern is illustrated in Figure 1, which plots the TMS-LF(blue line) and the optimal equity exposure (black line) during the out-of-sample evaluation period. Let us start from the most left point A in the figure, where both the TMS-LF and the optimal equity exposure are at their maximum. After point A, the TMS-LF starts to decrease while the optimal equity exposure still stays at its maximum for approximately four more years (until point B), after which the equity exposure starts to decrease. At point C the TMS-LF reaches its relative minimum, while the equity exposure continues to decrease and reaches its relative minimum immediately before the beginning of the recession. It stays around that level until the end of the recession (point D), after which it starts to increase again. After point D, approximately the same lead-lag pattern restarts. Interestingly, this pattern does not seem to be altered by the quantitative easing policy of the Federal Reserve in the latter part of the sample.
Figure 1 Equity weights and low-frequency component of the TMS
Note: This figure plots the dynamics of the low-frequency component of the term spread (blue line) and the equity weight (black line) for a mean-variance investor who allocates monthly his or her wealth between equities and risk-free bills according to a portfolio rule using stock return forecasts based on the low frequency of the term spread. For readability, the series of the low-frequency component of the term spread has been demeaned and centered around 1. Gray bars denote NBER-dated recessions. The in-sample period is January 1973 to December 1989, and the out-of-sample evaluation period is from January 1990 to December 2017.
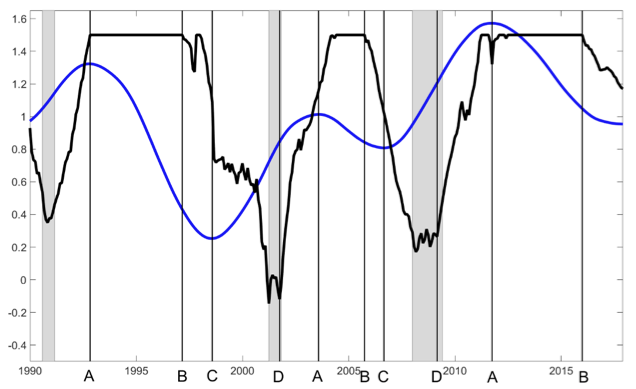
A trading strategy based on the ERP forecast using the low frequency of the TMS thus shows a strong market timing ability. This contrasts with the poor market timing of a trading strategy based on ERP forecasts using the TMS, as illustrated in Figure 2.
Figure 2 Equity weights and the TMS
Note: This figure plots the dynamics of the term spread (blue line) and the equity weight (black line) for a mean-variance investor who allocates monthly his or her wealth between equities and risk-free bills according to a portfolio rule using stock return forecasts based on the term spread. For readability, the series of the term spread has been demeaned and centered around 1. Gray bars denote NBER-dated recessions. The in-sample period is January 1973 to December 1989, and the out-of-sample evaluation period is from January 1990 to December 2017.
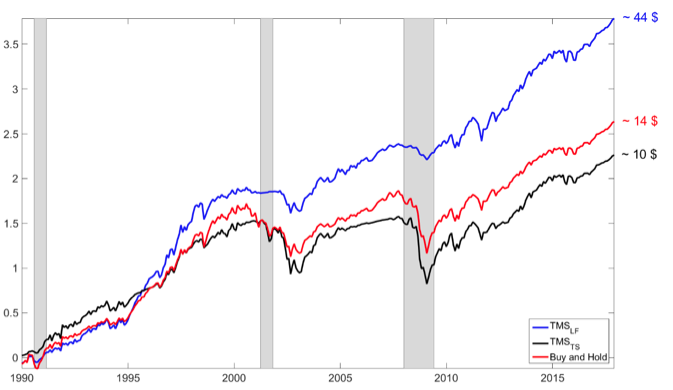
Consistently, Figure 3 shows that a trading strategy based on the low-frequency (long-term) dynamics of the TMS is much more profitable than the one based on the TMS. In other words, it pays off to be focused on the long-term dynamics of the TMS and to ignore its higher-frequency fluctuations. Figure 3 also shows that the buy-and-hold strategy is much less profitable than the strategy based on the low frequency of the TMS.
Figure 3 Log cumulative wealth
Note: This figure plots the log cumulative wealth for a mean-variance investor who allocates monthly his or her wealth between equities and risk-free bills according to a portfolio rule using stock return forecasts based on the low-frequency component of the TMS (blue line), the original time series of the TMS (black line), and the buy-and-hold strategy (red line), assuming that the investor begins with 1$ and reinvest all proceeds. Gray bars denote NBER-dated recessions. The in-sample period is January 1973 to December 1989, and the out-of-sample evaluation period is from January 1990 to December 2017.
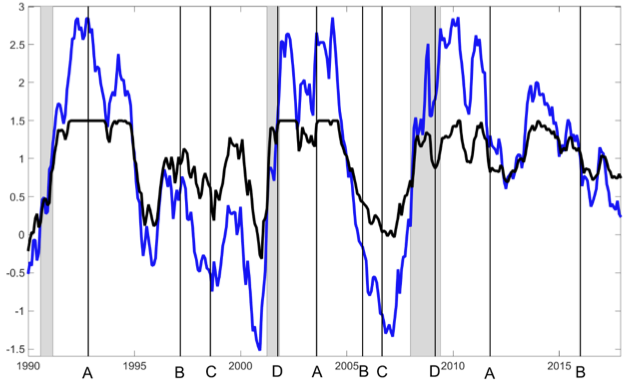
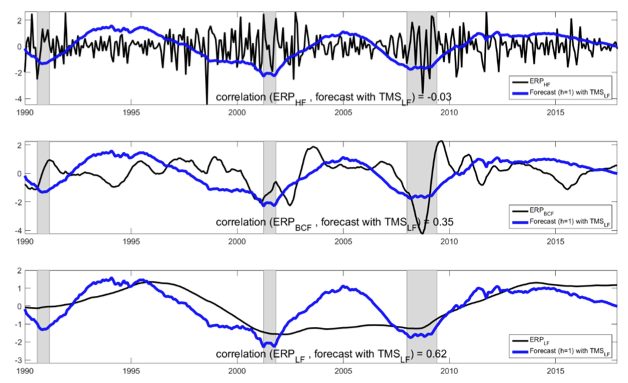
Another possible reason for the good predictive power of the TMS-LF comes from Figure 4, which reports the dynamics of the one-month ahead ERP forecast using the TMS-LF and the high-frequency, business-cycle-frequency and low-frequency components of the ERP (top, middle, and bottom graph, respectively). It is clear that the predictability power of the TMS-LF comes essentially from its ability to capture the low-frequency dynamics of the ERP. In fact, the correlation between the forecast with the TMS-LF and the low-frequency component of the ERP is 0.62, while the correlation between the forecast with the TMS-LF and the other frequency components of the ERP is much lower. This is in line with recent empirical evidence (Bianchi et al. 2017) showing that there are low-frequency, decades-long shifts in asset values relative to measures of macroeconomic fundamentals in the US.
Figure 4 ERP frequency components and ERP forecast based on the TMS-LF
Note: This figure plots the dynamics of the one-month ahead equity risk premium (ERP) forecast based on the low-frequency component of the term spread (blue line) and the high-frequency, business-cycle-frequency and low-frequency components of the ERP (top, middle and bottom graphs, respectively, black lines). The series are centered to have zero mean and scaled to have standard deviation 1. Gray bars denote NBER-dated recessions. The out-of-sample evaluation period is from January 1990 to December 2017
Practical implications
Bianchi et al. (2017) show evidence that ‘breaks’ in the mean of the consumption-wealth variable (as introduced by Lettau et al.2001) are strongly associated with low-frequency fluctuations in the real value of the Federal Reserve's primary policy rate, with low policy rates associated with high asset valuations and vice versa. Furthermore, Cieslak and Vissing-Jorgensen(2017) show that stock returns are a statistically more powerful predictor of Federal funds target changes than macroeconomic news releases. In particular, they analyse the economics of the tendency for low stock returns to predict accommodating monetary policy (the ‘FED put’ policy), claiming that the focus on the stock market primarily reflects the Fed’s concern about the consumption-wealth effect and about the impact of the stock market movements on investment. Therefore, for policymakers interested in gauging equity market developments, the low frequency of the term spread can be a very promising variable to look at.
References
Bianchi, F, M Lettau, and S Ludvigson (2017), “Monetary policy and asset valuation”, CEPR Discussion Paper no. 12275.
Campbell, J Y (1987), “Stock returns and the term structure”, Journal of Financial Economics, 18 (2), 373-399.
Cieslak, A, and A Vissing-Jorgensen (2017), “The economics of the Fed put”, April.
Chen, N-F, R Roll, and S A Ross (1986), “Economic forces and the stock market”, Journal of Business, 59 (3), 383-403.
Dew-Becker, I, and S Giglio (2016), “Asset pricing in the frequency domain: theory and empirics”, Review of Financial Studies, 29 (8), 2029-2068.
Fama, E F, and K R French (1989), “Business conditions and expected returns on stocks and bonds”, Journal of Financial Economics, 25 (1), 23-49.
Faria, G, and F Verona (2018), “The equity risk premium and the low frequency of the term spread”, Bank of Finland Research Discussion Papers 7/2018.
Goyal, A, and I Welch (2008), “A comprehensive look at the empirical performanceof equity premium prediction”, Review of Financial Studies, 21(4), 1455-1508
Lettau, M, and S Ludvigson (2001), “Consumption, aggregate wealth, and expected stock returns”, Journal of Finance, 56(3), 815-849
Rapach, D E, and G Zhou (2013): “Forecasting stock returns”, vol 2 of Handbook of Economic Forecasting, 328-383 Elsevier.
Endnotes
[1] During the sample period under analysis, the correlation between the low-frequency components of the long- and short-term interest rates is 0.99, while it is negative between them and the TMS (-0.51 and -0.63, respectively). So, an increase in the TMS-LF tends to coincide with decreasing interest rates and, hence, with increasing equity valuation.