Exams have been used for millennia to evaluate the ability of the test takers, allocate workers to jobs, and grant educational opportunities to students. A widely used form is the multiple choice exam, where the takers simply select one of a finite list of possible answers. This style of exam is attractive to educators due to the speed and precision with which exams can be graded. However, it is often criticised due to the fact that test takers can guess – a correct answer does not necessarily indicate understanding. This reduces the precision of the test – guessing behaviour adds noise to the exam score, which impedes the efficiency of the allocation process (Baker et al. 2010).
One approach to reducing such noise in the exam score is to have penalties for the wrong answer – students are allowed to skip a question, but should they answer incorrectly, they lose points.1,2 This discourages guessing when the student is unsure of the correct answer, and more so the more risk averse the student is. If a student is not risk averse and the penalty is such that a random guess gives zero, he will guess if he thinks one answer is the best, no matter how sure he is of the answer. However, a more risk-averse student will only guess if he is ‘sure enough’ of the best answer, and will skip otherwise. This raises the average score of the less risk averse relative to the more risk averse. While negative marking should lead to a more accurate measure of ability (Espinosa and Gardeazabal 2010), yielding an admitted class of a higher calibre, it has a cost as it discriminates against the more risk averse. Negative marking has been used in Turkish university entrance exams, Finnish entrance exams, and (until recently) the SAT.3
Risk aversion and gender
If attitudes towards risk differ a lot by gender, with women being more risk averse (Eckel and Grossman 2008), negative marking in effect biases the test against women who will tend to skip more often, thereby reducing their expected score and their chances of a successful outcome (Pekkarinen 2014, Tannenbaum 2012, Baldiga 2013). As such, an important question is the trade-off between precision and fairness in the real world.
In recent work, we approach this question using data from the Turkey university admission exam (ÖSS) (Akyol et al 2016). This is a high-stakes exam that applies penalties to incorrect answers, so that the expected score of a random guess is equal to zero. While a correct answer yields a single point, choosing one of the four incorrect answers reduces the score by 0.25 points. This is a rare example of a real life high-stakes setting where risk aversion plays a large role.
In standard scoring regimes, the test taker simply chooses the answer most likely to be correct (randomising if necessary). However when penalties are applied, they must decide whether to answer or not. The following advice is often provided: “You should never guess randomly on the SAT. However, if you can rule out at least one answer choice on a question you don't know, it is worth it to guess.”4
We estimate test-taking behaviour in the Turkish university entrance exam (Akyol et al. 2016). We take the view that in many circumstances, the above rule is not necessarily helpful. A student might not be able to rule out a given answer, yet they may have an unfavourable view of its likelihood of being correct. However, there will likely be an answer that is the test taker’s least favourite option – although all of the answers may be plausible, they are not equally plausible. Conversely, there will be an answer, the one the test taker considers the most likely, the one she would choose were there no penalty. Suppose the most likely to be correct answer is considered to have a 30% chance of being correct. Should the student choose that answer? Or should they skip? We define a threshold, c, which is the likelihood of the answer being correct. Above this threshold, students would attempt the question with more risk-averse students having a higher threshold. For the purpose of the test, c captures the risk preferences.
Modelling the decision
We explicitly model the test-taking behaviour of students, and use this model to estimate their risk preferences – the aforementioned threshold.
We allow this threshold to depend on both gender and the calibre of the student. While top students may be extremely concerned with the prospect of losing fractions of points and therefore reducing the chance of admission into a top school and so be risk averse, students of lesser ability would perhaps fail to gain admission if they receive their expected score, and perhaps even be risk loving.
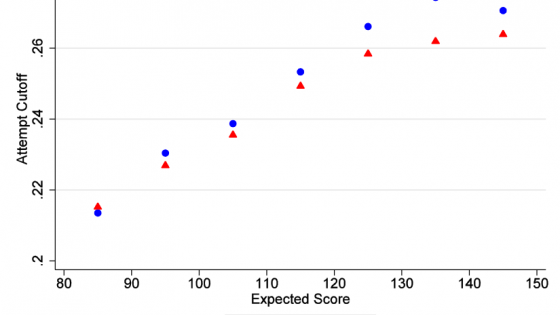
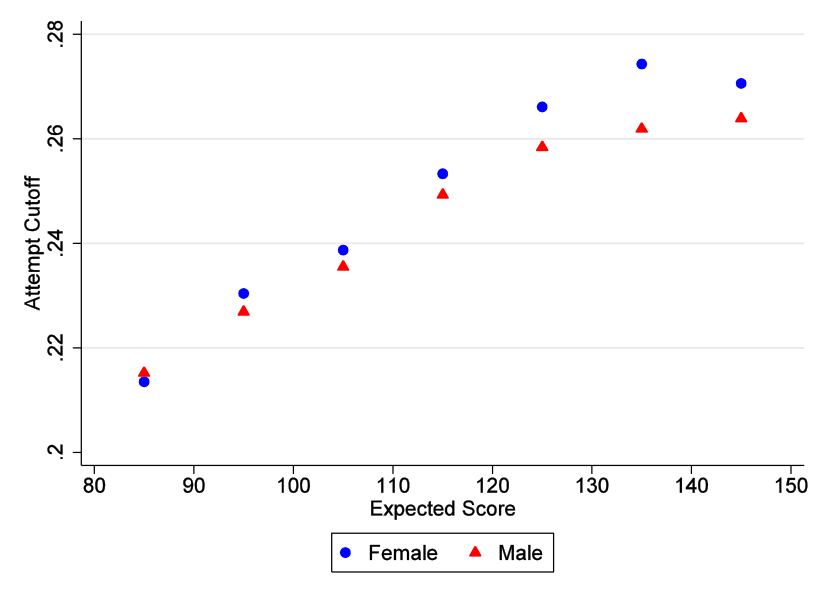
Consistent with prior expectations, we find that women are more risk averse. As shown in Figure 1, which plots the estimated value of c for men and women with different expected scores (ability), risk aversion increases with score and at all scores women require a greater degree of certainty to be willing to answer a question. The differences between genders are statistically significant for the most part, but are relatively small. In the data, there are five possible answers, so that while a random guess has a 20% chance of success; a high ability man would skip unless he was approximately 26% sure, whereas a high ability woman would need to be 27% sure.
Figure 1. The cut-off: The anticipated chance of success below which a test taker would skip, by gender and expected score
How important is the gender bias?
Having obtained risk preferences, we are able to use the model to perform counterfactuals, to see how outcomes would change under alternative exam structures. We examine several exam structures to answer what would happen to the allocation of students to universities. For example, what is the impact of removing the penalty, increasing the penalty or perhaps increasing the number of questions?
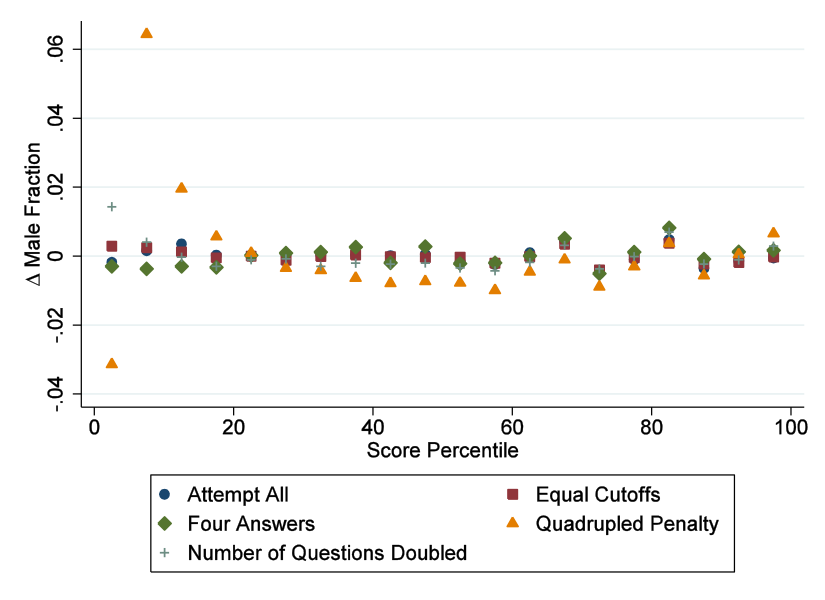
We simulate outcomes and examine the composition of score groups, for example the proportion of males in the top 5% of scorers. We find that the effect on the gender ratio (the proportion of males) in a given score percentile group is minimal – risk aversion differences have a negligible impact on outcomes. As seen in Figure 2, the gender ratio in the top scoring groups is largely invariant across test regimes.
Figure 2. Male fraction of students in various score percentiles under alternate test regimes, compared to the baseline model
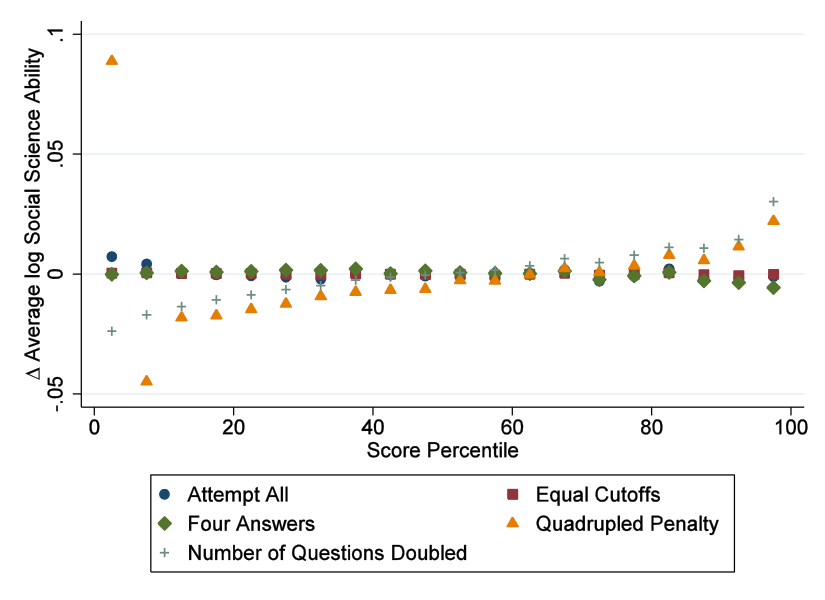
We do find that the penalty does lead to more precision – the ability of students in the top score percentiles increases as we increase the penalty and decreases if we remove the penalty. This is shown in Figure 3, where the ability of the top performing students is higher when students are sorted using an exam with a high penalty, or with more questions (while the latter trivially increases the accuracy of a test, it is costly). Thus, penalties lead to an admitted class of greater quality. In fact, we find that increasing the penalty from 0.25 points to 1 point is similar to increasing the length of the exam from 45 to 70 questions!
Figure 3. Social science ability of students in various score percentiles under alternate test regimes, compared to the baseline model
Why do risk aversion differences seem to matter so little? For these differences to matter, two things have to happen. First, the best choice has to have a probability of being correct that lies in the gap in their c – that is, between .26 and .27. Thus, there is a relatively low chance that the differences will be relevant for a given question as the gap between cut-offs is small. Moreover, even if the belief does lie in this region, the expected gain from answering is very small as test takers are not very risk averse. Essentially, differences in choices made due to skipping behavior are not common, and when they do arise, have small consequences. Intuitively, this is like saying that while ordering at a restaurant, the best option is usually clear, and when it is not, the choice made is of little consequence!
References
Akyol, S P, J Key and K Krishna (2016) “Hit or miss? Test taking behavior in multiple choice exams”, NBER, Working Paper 22401.
Baker, E L, P E Barton, L Darling-Hammond, E Haertel, H F Ladd, R L Linn, ... & L A Shepard (2010) “Problems with the use of student test scores to evaluate teachers”, EPI Briefing Paper# 278, Economic Policy Institute.
Espinosa, M P and J Gardeazabal (2010) “Optimal correction for guessing in multiple-choice tests”, Journal of Mathematical Psychology, 54(5): 4.
Pekkarinen, T (2015) “Gender differences in behaviour under competitive pressure: Evidence on omission patterns in university entrance examinations”, Journal of Economic Behavior & Organization, 115: 94-110.
Baldiga, K (2013) “Gender differences in willingness to guess”, Management Science, 60(2): 434-448.
Eckel, C C and P J Grossman (2008) “Men, women and risk aversion: Experimental evidence”, Handbook of experimental economics results, 1: 1061-107.
Endnotes
[1] There are other approaches, such as the proper scoring rule, whereby test takers reveal their belief regarding the likelihood of each answer being correct, however these are often challenging to use effectively in practice.
[2] Alternatively, do not penalise incorrect answers yet award a fraction of a point for skipping. This can be made to be equivalent in theory and in experimental evidence (Espinosa and Gardeazabal 2013).
[3] The penalty for incorrect answers was removed in March 2016, see here for more information.
[4] See http://www.math.com/students/kaplan/sat_intro/guess2.htm