Modern economies are characterised by a complex interfirm network structure. In such networks, a shock originated in a firm can cause a domino effect and travel throughout the economy. Acemoglu et al. (2012) show that if the degree (number of partners) distribution of a network is fat-tailed, firm-level idiosyncratic shocks can propagate to other firms and cause aggregate fluctuations. Their model provides a microfoundation for the ‘granular' origins of business cycles proposed by Gabaix (2011). Despite its importance, there is little empirical evidence on the structure of inter-firm production networks and shock propagation mainly due to the lack of data. A few exceptions include Carvalho et al. (2014) and Boehm et al. (2015). They both study the impact of supply chain disruptions caused by an earthquake in Japan and confirm that the shock propagates both domestically and internationally. Unlike their specifications, this research does not investigate the causal evidence of shock propagations. Rather, it examines the buyer-supplier sales comovements at a large scale to provide more comprehensive evidence.
Production networks and sales growth
In a recent paper (Fujii 2016), I use Japanese firm-level data compiled by a credit reporting company, which also is used in Carvalho et al. (2014). The dataset covers about one million firms, and three years (2006, 2011, and 2012) of data are analysed. For each firm, it reports sales, sales growth, number of employees, headquarters address, industry classification, and so forth. The unique feature of this dataset is the large-scale interfirm network data. Firms report their suppliers and customers up to 24 partners. Despite this truncation threshold, we can capture the interfirm network quite well by merging self- and other-reported data. For some countries, this type of transaction network data is available only for listed firms or certain small industries. Unlike those, the Japanese data are comprehensive and cover almost all sectors and sizes.
As also reported in Bernard et al. (2014), out-degree (number of customers) and in-degree (number of suppliers) are well approximated by a Pareto distribution, meaning that some firms have thousands of partners while a large majority of firms have only one or two partners. This underscores the disproportionately large influence of well-connected firms on aggregate fluctuations as pointed out by Acemoglu et al. (2012). The log of sales and sales growth rate both follow the normal distribution. To see the relationship between size, degree, and sales growth, firms are first divided into 100 groups based on their sales volume. In all years, larger firm groups exhibit higher mean growth rates and lower dispersions. I conduct the same exercise based on degrees as well. Well-connected firms show higher sales growth, but no clear pattern is confirmed between degree and sales dispersion.
Buyer-supplier comovements in a production network
This section investigates buyer-supplier sales comovements in the Japanese production network. There are many studies that estimate the degree of shock propagation using industry-level input-output (I-O) matrix or international I-O table for intermediate goods, but little research has quantified the buyer-supplier comovements using large-scale production network data. Due to the network feature of the model, I apply estimation techniques developed in spatial econometrics literature.
The first question we need to ask is: Is there any buyer-supplier interdependence in firms’ sales growth rates? To answer this, I compute Moran’s I statistic. This statistic shows if there exists a statistically significant relationship between firms’ sales growth rates and their suppliers’ (or customers) growth rates. In all years, I confirm strong network interdependence for both types of network. A firm’s growth rate is affected by its suppliers and customers.
To estimate the magnitude of partners’ effects, I regress firm sales growth on the average growth of partners and other control variables such as the number of employees, credit score, age, and industry fixed effects. Since the data do not provide the dollar amount of transactions, the partners’ growth rate is computed with equal weights. I call the coefficient of the partners’ growth the “propagation factor”, denoted by lambda. In this specification, the vector of sales growth appears on both left- and right-hand sides, causing an endogenous bias. A spatial autoregressive (SAR) model with instrument variables is used to consistently estimate the parameter. In all years, the upstream propagation factor is larger than the downstream factor. In 2012, the elasticity of average sales growth of suppliers is 0.153, while that of customers is 0.257. The higher degree of upstream propagation implies that it is more difficult to replace an existing customer or adjust to a demand shock.
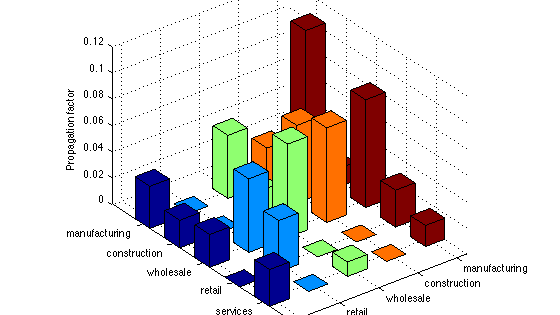
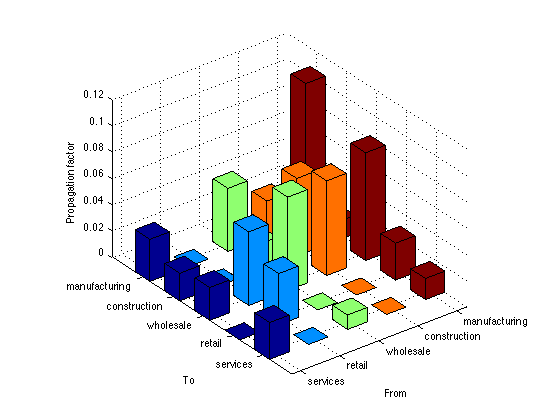
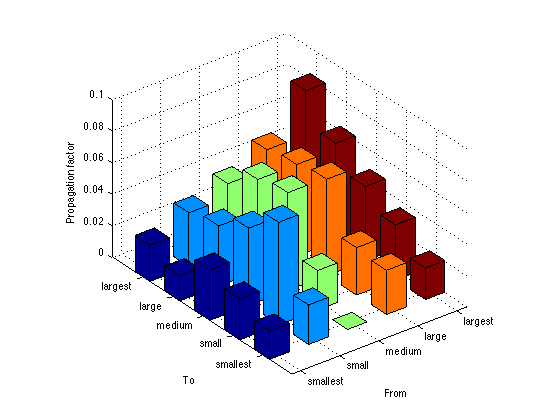
I extend the econometric model to incorporate heterogeneous propagation factors across different groups of firms. For this exercise, two types of groups are considered: industry (manufacturing, construction, wholesale, retail, and services) and size (largest, large, medium, small, smallest). Figures 1 and 2 display the estimated group-specific downstream propagation factors.
Figure 1
In Figure 1, the diagonal elements are all positive and significant implying the existence of within-sector propagations. The manufacturing-to-manufacturing pair has the highest propagation factor. The wholesale sector tends to be affected by suppliers, and the impact is largest if the supplier is a manufacturer, and smallest if the supplier is in the service sector. Firms in retail and service sectors neither receive nor propagate downstream shocks to their transaction partners. Cravino and Levchenko (2014) also found stronger sales comovements between multinational firms and their foreign affiliates in the manufacturing sector compared to the service sector. In the manufacturing sector, the interdependence of intermediate physical inputs produced by other firms may generate an additional margin for the buyer-supplier comovements.
Figure 2
Figure 2 shows that the largest size group has higher propagation factors with the largest-to-largest pair being the highest. If we focus on the row of the largest group, we see a decreasing pattern from the largest to the smallest. In general, larger firms have a relatively greater impact on their partners, and the effect is stronger if the partners are also large. In sum, larger firms in a manufacturing sector tend to propagate shocks through a production network. These empirical facts should be remembered when considering a bailout or fiscal stimulus for a particular group of firms.
References
Acemoglu, D, V M Carvalho, A Ozdaglar, and A Tahbaz-Salehi (2012) “The Network Origins of Aggregate Fluctuations,” Econometrica, Vol. 80, No. 5, pp. 1977–2016.
Bernard, A B, A Moxnes, and Y U. Saito (2014) “Geography and Firm Performance in the Japanese Production Network,” RIETI Discussion Paper Series 14-E-034.
Bohem, C, A Flaaen, and N Pandalai-Nayar (2015) “Input Linkages and Transmission of Shocks: Firm-Level Evidence from the 2011 Tohoku Earthquake,” Working Paper.
Carvalho, V M. M Nirei, and Y U. Saito (2014) “Supply Chain Disruptions: Evidence from the Great East Japan Earthquake,” RIETI Discussion Paper Series 14-E-035.
Cravino, J and A A Levchenko (2015) “Multinational Firms and International Business Cycle Transmission,” Working Paper.
Fujii, D (2016) “Shock Propagations in Granular Networks,” USC-INET Research Paper No. 16-23.
Gabaix, X (2011) “The Granular Origins of Aggregate Fluctuations,” Econometrica, Vol. 79, No. 3, pp. 733–772.