Authors often claim the study of human happiness is one of the fastest growing research fields in economics in the past 20 years (Kahneman and Krueger 2006, Clark et al. 2008). By looking at what socioeconomic and other factors predict (or cause) people to report higher or lower scores on a subjective wellbeing (SWB) scale, researchers have added new insights to standard views in economics.
This includes, for example, the wellbeing evidence of relative income (Clark and Oswald 1996), loss aversion (Boyce et al. 2013), and social norms (Clark 2003). Wellbeing research also suggest that inferences from individuals’ revealed preferences alone may not be sufficient to inform policymakers about what really matters to people’s overall quality of life. This calls for a regular collection of data on individuals’ SWB by offices of national statistics around the world to be used as one of the main target outcomes in policy design (Clark et al 2018).
As with any new and emerging research field, wellbeing research has attracted criticism, for example over the interpersonal incomparability of observed and latent wellbeing. Several studies have provided descriptive evidence that wellbeing responses are comparable from one person to another (Oswald and Wu 2010). But recent critiques of the SWB scales have shown that average ranking of both observed and latent happiness across groups can be arbitrarily reversed unless some unreasonably strong conditions are assumed (Schröder and Yitzhaki 2017, Bond and Lang, forthcoming).
The consequences of these critiques is potentially huge for most (if not all) of existing findings in wellbeing research, given that parameters from OLS and ordered probit/logit models, the typical regression for wellbeing estimations, are estimates of the average effects.
Mean ranking of ordinal data can be demanding for the data
The issue with comparing mean SWB scores across groups comes from the fact that SWB is an ordinal variable; for example, the life satisfaction question in the British Household Panel Surveys asked respondents to state on a 7-point scale how satisfied they are with their life overall, ranging from “1. Very dissatisfied” to “7. Very satisfied”.
Hence, the ranking of mean SWB scores is valid if, and only if, the ranking is stable for all increasing transformations of the wellbeing scale. The technical requirement for this is that there needs to be a first order stochastic dominance (FOSD) of SWB across groups. It may not be surprising that a direct mean ranking between reported SWB between two groups, as well as the sign of slope parameters in a regression, may change when we change the reported SWB scale, because these methods treat ordinal data like a cardinal variable.
Mean comparisons from an ordered choice model, such as the probit, are also susceptible. For example, suppose we have self-reported SWB levels of individuals from two groups – say, men and women. Assume that wellbeing is derived from a latent SWB variable that is drawn from a normal distribution. If the normal distributions of the two groups have different means and variances, then there is no FOSD. Then if, say, the mean SWB of women is higher than men, there always exist log-normal distributions obtained from taking an exponential transform of the latent SWB of men and women so that the mean SWB of men is higher than women.
Have econometric analyses of happiness data been futile?
The reversal of the mean ranking can happen with transformations – not only to the observed SWB scores, but also to the latent SWB of individuals. Unfortunately, the failure of FOSD is a norm rather than exception to the rule. An open question then arises whether the econometric analyses routinely conducted on SWB data over the decades have been futile. Using ordered probits, Bond and Lang (forthcoming) demonstrate this by taking on nine of the most well-known empirical results from the wellbeing literature. For each case, they were able to show that variances across groups differ and all the results, including the famous Easterlin Paradox – that an increase in income for all does not improve the aggregate happiness in the US over time (Easterlin 1974, 2017) – can be reversed by skewing the distribution of SWB scores away from normality.
There is currently no practical suggestion as to how best to analyse SWB data if we cannot straightforwardly rely on the usual analysis of mean comparisons.
Focus on the median, not the mean
Our latest work (Chen et al. 2019) proposes a novel solution to the problem: focus on the median, not the mean. Like the mean, the median is a centrality measure of a distribution. Yet, unlike the mean, the median respects the ordinal property of SWB data because it is equivalent to all increasing transformations. This suggests that the ranking of the medians is stable through any increasing transformation, thus freeing us from the burden of stochastic dominance conditions that we face when by making mean comparisons.
Computing the median can be very straightforward. For example, if the underlying latent distribution of SWB across groups in an ordered probit or logit model is symmetric, the median and therefore the mean of SWB scores are the same. So we can reinterpret the usual ordinal model’s estimates as the effects of the explanatory variables on the median rather than the mean. We emphasise here that heteroscedasticity should be explicitly accommodated to avoid assuming FOSD a priori. Subsequently, all the pre-transformed probit estimates in Bond and Lang's paper that are consistent with prior results in the wellbeing literature do not provide any contradiction when they are interpreted as medians instead of means.
The parametric assumption as well as the symmetry condition can be relaxed to just a zero median restriction. A semiparametric median regression of such ordered choice model can be estimated analogous to Manski’s maximum score estimator (Manski 1975, Lee 1992), but it is a notoriously difficult computational task (Pinkse 1993).
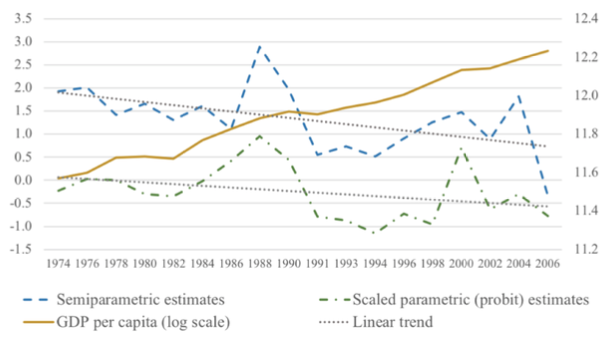
We have developed a novel constrained mixed-integer optimisation procedure for this latter case. Figure 1 suggests that, using 3-point scale happiness scores (1. Not too happy, 2. Pretty happy, 3. Happy) in the US General Social Survey, Easterlin’s Paradox continues to hold in the case of both parametric and semiparametric median models.
Figure 1 Support for the Easterlin Paradox using median models
Source: Chen et al. (2019) using data for US General Social Survey.
Notes: Parametric (probit) and semiparametric estimates. Median happiness scores (left axis) and log real GDP per capita (right axis).
The way forward
Researchers working with SWB data may find it tempting to ignore or even dismiss recent critiques as theoretical pedantry. But the argument persists that the mean comparison results that form the basis of empirical studies in the wellbeing literature have no empirical content.
We have provided a pragmatic solution to this issue by focusing on the median. By exploiting the fact that the mean and median of symmetric distributions are identical, parametric ordered response models that economists are familiar with can be analysed as usual when estimates are interpreted as the median rather than the mean.
Our argument, for example, ensures that leading prior studies in the wellbeing literature looked at by Bond and Lang remain valid without any additional work. We also show more sophisticated statistical methods can be used to estimate the median if we do not wish to impose parametric or symmetry assumptions.
Our advocacy of the median regression is not exclusively for analysing SWB data. The arguments and results apply to all types of categorical ordered data, such as health indicators and risk preferences. We also expect the inference on semiparametric median regression and large-scale estimation to become more feasible as computing hardware becomes more powerful, and solver algorithms for mixed integer optimisation problems improve.
References
Bond, T N, and K Lang (forthcoming), "The sad truth about happiness scales", Journal of Political Economy.
Boyce, C J, A M Wood, J Banks, A E Clark, and G D Brown (2013), "Money, well-being, and loss aversion: Does an income loss have a greater effect on well-being than an equivalent income gain?", Psychological Science 24(12): 2557-2562.
Chen, L Y, E Oparina, N Powdthavee, and S Srisuma (2019), "Have Econometric Analyses of Happiness Data Been Futile? A Simple Truth About Happiness Scales", IZA discussion paper 12152.
Clark, A E (2003), "Unemployment as a social norm: Psychological evidence from panel data", Journal of Labor Economics, 21(2): 323-351.
Clark, A E, S Flèche, R Layard, N Powdthavee, and G Ward (2018), The origins of happiness: the science of well-being over the life course, Princeton University Press.
Clark, A E, P Frijters, and M A Shields (2008), "Relative income, happiness, and utility: An explanation for the Easterlin paradox and other puzzles", Journal of Economic Literature 46(1): 95-144.
Clark, A E, and A J Oswald (1996), "Satisfaction and comparison income", Journal of Public Economics 61(3): 359-381.
Easterlin, R A (1974), "Does economic growth improve the human lot? Some empirical evidence", in P A David and M W Reder (eds), Nations and households in economic growth, Academic Press.
Easterlin, R A (2017), "Paradox Lost?" Review of Behavioral Economics 4(4): 311-339.
Kahneman, D, and A B Krueger (2006), "Developments in the measurement of subjective well-being", Journal of Economic Perspectives 20(1): 3-24.
Lee, M J (1992), "Median regression for ordered discrete response", Journal of Econometrics 51: 59–77.
Manski, C F (1975), "Maximum score estimation of the stochastic utility model of choice", Journal of Econometrics 3: 205–228.
Oswald, A J, and S Wu (2010), "Objective confirmation of subjective measures of human well-being: Evidence from the USA", Science 327(5965): 576-579.
Pinkse, C A P (1993), "On the computation of semiparametric estimates in limited dependent variable models", Journal of Econometrics 58: 185–205.
Schröder, C, and S Yitzhaki (2017), "Revisiting the evidence for cardinal treatment of ordinal variables", European Economic Review 92: 337-358.