Over the last three decades, most economists and central bankers have come to doubt the usefulness of money supply measures for conducting monetary policy, and have turned to macroeconomic models in which monetary aggregates have no role.
What was the main reason behind this move away from monetary aggregates? In our view, it was the alleged disappearance, starting from the early 1980s, of any previously identified stable relationship between monetary aggregates, GDP, and interest rates. For the US, for example, researchers such as Friedman and Kuttner (1992) have documented the breakdown during those years of any stable long-run demand for several alternative monetary aggregates. By the same token, in the Eurozone, the ECB’s so-called monetary pillar (a reference value for the annual growth rate of M3 derived from a money demand equation) has come to be seen as too unreliable to be of any use at all.
There is a clear sense in which this move away from monetary aggregates has left monetary policy untroubled. Over the same decades, there was a surge in the number of central banks that were explicitly or implicitly following inflation-targeting policies in which the monetary policy instrument was the short-term interest rate. And the result has clearly been remarkable – inflation has been defeated. This has been the case for developed economies that saw their inflation rates climb to two digits for a few years in the late 1970s and early 1980s, for emerging economies that experienced hyperinflation during the same years, and for everything in between. In 2015, with a yearly inflation rate of around 30%, Argentina had one of the highest inflation rates in the world – a rate that, ironically, would have been one of the lowest in Latin America in the 1980s.
In this column, we first review recent work on the long-run demand for money, and argue that it is alive and well. We then explain why we believe that this finding may contribute to the monetary policy debate.
In a recent paper, using a specific, narrow monetary aggregate, M1,1 we study a dataset comprising 32 countries since the mid-19th century (Benati et al. 2016). The main finding of this large-scale investigation is that, contrary to conventional wisdom, in most cases statistical tests do identify with high confidence a long-run equilibrium relationship between either M1 velocity2 and a short-term interest rate, or M1, GDP, and a short rate – that is, a long-run money demand.
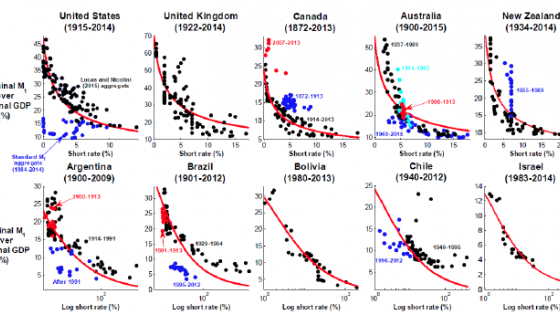
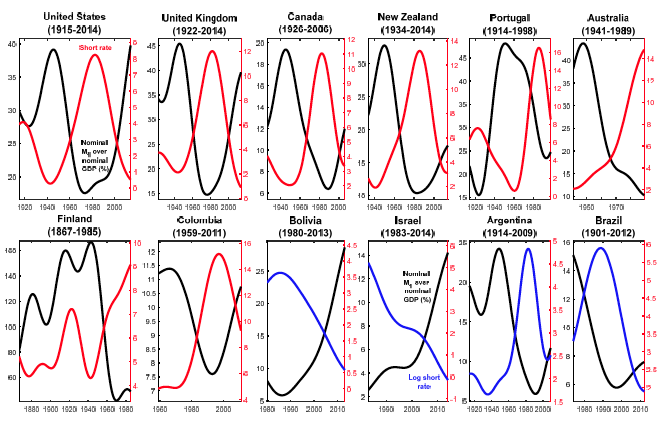
Figure 1. The raw data: Short rate (plus 1%), ratio between nominal M1 and nominal GDP, and fitted Baumol-Tobin specification
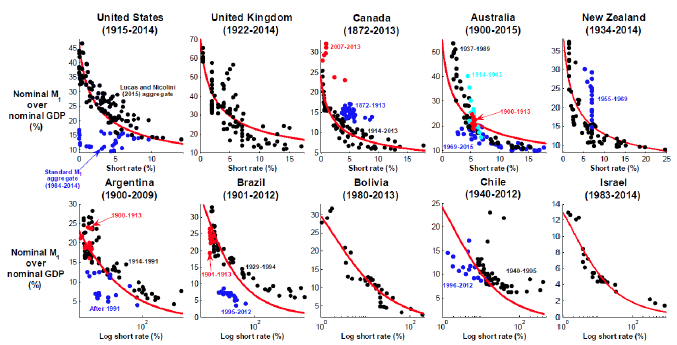
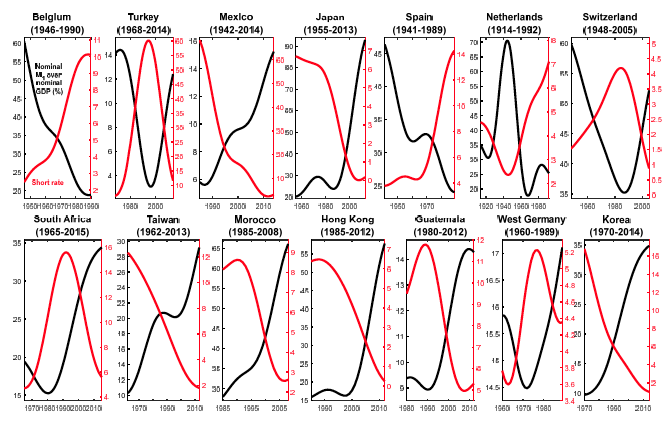
Figure 2. The raw data: Short rate (plus 1%), ratio between nominal M1 and nominal GDP, and fitted Baumol-Tobin specification
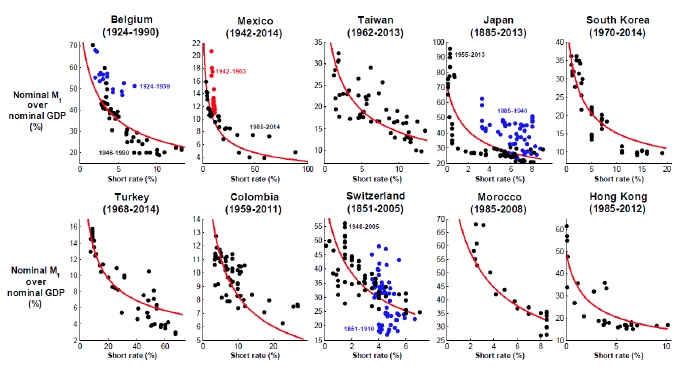
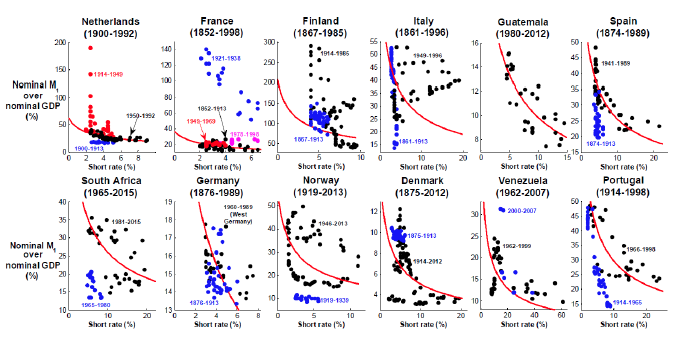
Figure 3. The raw data: Short rate (plus 1%), ratio between nominal M1 and nominal GDP, and fitted Baumol-Tobin specification
Figures 1 to 3 show scatterplots of a short-term interest rate3 and the ratio between nominal M1 and nominal GDP (that is, the inverse of M1 velocity), together with the theoretical money demand curve predicted by the classic Baumol (1952) and Tobin (1956) money demand specification. The latter implies a linear relationship between the logarithms of the two variables, with an elasticity of one half.4 We emphasise that the levels of the theoretical curves have been chosen to go through the data in each country. The slope of each curve, however, is the one predicted by the Baumol-Tobin theory – it was not chosen to match the data.
In all of the figures, the data are shown with different colours under four circumstances:
- to indicate data for the gold standard, which are always shown with a different colour from that used in subsequent years;
- when the data are for non-consecutive sub-periods (as in the case of Belgium, for example);
- when there are different series for the short-term interest rate that cannot be linked (as in the case of Australia, for example); and,
- to highlight changes either in the monetary regime or in the relationship between velocity and the short rate (as in the case of Portugal, for example).
Finally, for the US, we show two different measures. One is the standard definition of M1. The other is the one proposed by Lucas and Nicolini (2015), which is the sum of M1 plus money market deposit accounts that were created in 1982. This measure performs an economic function analogous to that of standard bank deposits, which have traditionally been included in M1.
We find the evidence reported in Figures 1 to 3 quite remarkable. Visual evidence is strong for several countries, including the UK, Canada, Australia, New Zealand,5 Bolivia, Israel, Belgium, Mexico, Japan, Switzerland over the post-WWII period, Morocco, Turkey, Hong Kong, and South Korea. As shown by Benati et al (2016), in many cases proper statistical tests6 do indeed confirm the visual impression of a stable relationship between the amount of M1 that is demanded by the private sector as a fraction of overall income and the opportunity cost of holding M1 balances.
Figure 4. Low-frequency components of short rate and ratio between nominal M1 and nominal GDP for selected countries
Figure 5. Low-frequency components of short rate and ratio between nominal M1 and nominal GDP for selected countries
Figures 4 and 5 present evidence in the spirit of Lucas (1980), Benati (2005) and Benati (2009), by plotting the low-frequency components of the same series shown in the scatterplots in Figures 1 to 3. The components have been extracted via the filter proposed by Christiano and Fitzgerald (2003). We find this evidence – which consistently points toward a negative correlation between the inverse of M1 velocity and the short rate at very low frequencies – quite simply remarkable. Although the main empirical body of our work is based on cointegration tests, the evidence in Figures 4 and 5 is possibly even more convincing because it is based on a simple technique such as linear filtering, which uniquely hinges on defining a specific frequency band of interest.
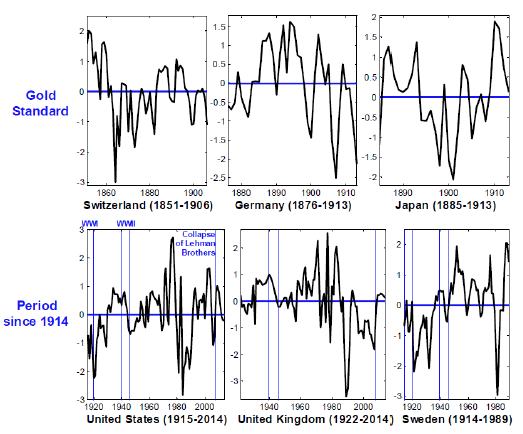
Although the evidence in Figures 1 to 3 and, especially, Figures 4 and 5 clearly points, in most cases, toward a long-run money demand relationship, such a relationship should quite obviously not be expected to hold on a period-by-period basis (within the present context, every single year). Long-run equilibrium relationships such as those discussed herein7 indeed imply temporary deviations that are bound to disappear in the long run. Figure 6 shows, for a few selected countries, and for either the gold standard period or the period since 1914, what such temporary deviations from the equilibrium implied by the long-run demand for M1 look like. In all cases (and in many more, documented in Benati et al. 2016), the deviations clearly appear as ultimately transitory, but at the same time they are quite persistent (i.e. long-lived), thus implying that deviations from the long-run relationship on the money market are typically long-lived.
Figure 6. Temporary deviations from the long-run equilibrium relationship between M1 velocity and the short rate
One may wonder whether this discussion offers anything relevant at all. After all, we all agree that the performance of central banks in the last three decades has been remarkably successful, even though they completely ignored monetary aggregates. So does this discussion just reflect intellectual curiosity?
We do not believe so. Since the Great Recession of 2008-2009, many central banks lowered their interest rates to their effective lower bound. Since then, balance sheets have grown without precedent. At the same time, fear of deflation and difficulties in creating inflation started to play an increasing role in the policy debates of major central banks. For many, the lower-bound trap for nominal interest rates is the result of private sector expectations that are not ‘anchored,’ where the central bank is left without control of the inflation rate.
Our evidence shows that, ultimately, the inflation rate can be controlled by properly managing monetary aggregates. And there is no doubt that central banks can control monetary aggregates.8 Thus, it suggests that there may be ways for the central bank to affect expectations by properly managing monetary aggregates and move the economy away from deflationary pressures. To some extent, our evidence suggests that the ‘helicopter drops’ that have recently been discussed in Europe, understood as directly managing monetary aggregates, are a tool that central banks could consider using.
Several caveats are in order. First, from a theoretical point of view, the way a helicopter drop affects the economy at the lower bound may be different from the way it operates when interest rates are positive. Second, from the point of view of the data, and as we explained above, our evidence points to the existence of a long-run relationship, but the short-run departures are large, persistent, and unexplained in these papers. Finally, correctly choosing the monetary aggregate in times of regulatory changes – as we have experienced since 2008 – is a difficult task, as Lucas and Nicolini (2015) point out.
Thus, we do not think that we are ready to take our findings to the policy debate yet. We do believe, however, that what we have so far justifies further study on how monetary aggregates can complement the toolkit of central banks, particularly following long periods of interest rates at their effective lower bound.
References
Alvarez, F and F Lippi (2009) “Financial innovation and the transactions demand for cash”, Econometrica, 77(2): 363–402.
Baumol, W J (1952) “The transactions demand for cash: An inventory theoretic approach”, Quarterly Journal of Economics, 66(4): 545–556.
Benati, L (2005) “Long run evidence on money growth and inflation”, Bank of England Quarterly Bulletin, Autumn.
Benati, L (2009): “Long run evidence on money growth and inflation”, ECB Working paper series no 1027.
Benati, L, R E Lucas Jr, J-P Nicolini and W Weber (2016) “International evidence on long run money demand”, NBER Working paper 22475.
Christiano, L J and T J Fitzgerald (2003) “The band pass filter”, International Economic Review, 44(2): 435–465.
Friedman, B M and K N Kuttner (1992) “Money, income, prices, and interest rates”, American Economic Review, 82(3): 472–492.
Lucas, R E, Jr (1980) “Two illustrations on the quantity theory of money”, American Economic Review, 70(5): 1005–1014.
Lucas, R E, Jr, and J-P Nicolini (2015) “On the stability of money demand”, Journal of Monetary Economics, 73(July): 48–65.
Tobin, J (1956) “The interest-elasticity of transactions demand for cash”, Review of Economics and Statistics, 38(3): 241–247.
Endnotes
[1] The monetary aggregate M1 is defined as the sum of currency and bank deposits.
[2] The velocity of a monetary aggregate is defined as the ratio between GDP in current prices and the monetary aggregate.
[3] For the very high-inflation countries in the bottom row of Figure 1, we show the logarithm of the short rate rather than its level in order to make the figure intelligible.
[4] Following Alvarez and Lippi (2009), we assume that cash entails a negative rate of return, associated with the risk of it being lost or stolen. This is why the theoretical money demand curve crosses the vertical axis at a finite ‘satiation level’ of money balances rather than exploding to infinity.
[5] With the exception of the period 1955–1969, during which the interest rate remained essentially unchanged.
[6] Specifically, so-called cointegration tests.
[7] So-called cointegration relationships.
[8] Naturally, because central banks do not directly control M1 but only high-power money, understanding the evolution of the money multiplier is necessary. Given the very low-frequency movements in the multiplier, this does not seem to be a serious problem.