Simple rules for monetary policy provide useful reference points for assessing a given policy stance. Importantly, Janet Yellen, Chair of the Board of Governors of the Federal Reserve System, has referred to such rules repeatedly, especially the Taylor rule. She has explained that such rules would be consistent with Fed policy if recent estimates of an equilibrium real interest rate (R-Star) near 0% by Holston et al. (2017) are taken into account (Yellen 2017). Similarly, ECB President Mario Draghi and ECB Vice-President Vítor Constâncio have argued that a low equilibrium real interest rate, rather than ECB policy, is to blame for the low interest rate environment in the Eurozone (Draghi 2016, Constâncio 2016). The equilibrium rate is thought to have declined this much in order to equilibrate the supply of savings with the demand for investment purposes for the medium to long run.
Yet, as shown in Beyer and Wieland (2017), estimates of the medium-run equilibrium real rate in the vein of Laubach and Williams (2003) are extremely imprecise and highly sensitive to seemingly innocuous technical assumptions (see also Michaelis and Wieland 2017, Taylor and Wieland 2016). Thus, the ‘true’ equilibrium rate may just as well not have declined as much as these estimates did in recent years. In this case, the low interest rate environment is predominantly due to easy monetary policy including central bank asset purchases, and simple rules would call for an exit from this policy. In fact, an application of the Taylor (1993) rule to the Eurozone calls for an exit from quantitative easing even if one uses the low R-Star estimate in the rule, as long as the consistent output gap estimate obtained with the same method is also used.
The Taylor rule (Taylor 1993) prescribes a central bank rate that is the sum of four components: the long-run equilibrium real interest rate, the rate of inflation, the deviation of inflation from the target multiplied with a reaction coefficient of ½, and the percentage deviation of actual from potential GDP (output gap) multiplied with a reaction coefficient of ½.
Prior to the Global Crisis, this rule signalled that US Fed funds rates remained too low for too long (Taylor 2007), and it calls for policy tightening at the current juncture. Hence, Yellen (2017) argues: “if the neutral rate were to remain quite low over the medium term, … then the appropriate setting for R-Star in the Taylor rule would arguably be zero, yielding a yet lower path for the federal funds rate”.
ECB policy, rules and R-Star
In 2013, the ECB announced that the “Governing Council expects ECB interest rates to remain at present or lower levels for an extended period of time” (Draghi 2013a), and ECB President Mario Draghi said, “As a matter of fact, you can … extract a reaction function and from there estimate, what would be a reasonable extended period of time” (Draghi 2013b). Indeed, past changes in ECB interest rates can largely be explained with a simple reaction function. This reaction function or rule calls for changing the policy rate whenever the inflation forecast deviates from target and the output growth forecast from potential. In each case, the reaction coefficient is ½.
This first-difference rule did not call for massive quantitative easing in 2015/16 (Bletzinger and Wieland 2016). Furthermore, it does not support the ECB’s case for policy easing in response to low R-Star estimates, because it neither includes nor requires an R-Star. This is a big advantage, because estimates of medium-run equilibrium rates in the vein of Laubach and Williams (2003), Garnier and Wilhelmsen (2009) and Holston et al. (2017) are extremely imprecise.
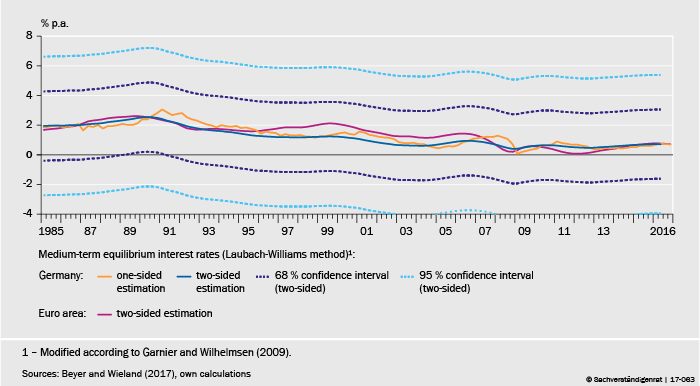
Figure 1 Estimates for medium-run equilibrium interest rates in Germany and the Eurozone
In Figure 1, estimates according to Beyer and Wieland (2017) indicate 68% confidence intervals of +/- 2.33% for two-sided estimates. Of course, the most recent one-sided estimates are even more imprecise. Point estimates reported by Beyer and Wieland (2017) have declined. In 2016, they stand at 0.7%, relative to -1.5% in Holston et al. (2017). Yet, given the lack of precision actual values may not have changed at all. Furthermore, seemingly innocuous technical assumptions result in quite different point estimates indicating a high degree of instability. Additionally, they may suffer from omitted variable bias (Taylor and Wieland 2016, Cukierman 2016). Thus, it would be better not to use them as a key determinant of the policy stance. Instead, one could use estimates of long-run equilibrium rates as in the original Taylor rule, which have not changed as much.
If policymakers nevertheless wish to use these medium-run R-Star estimates, they should use them together with the consistent output gap estimates. This makes quite a difference.
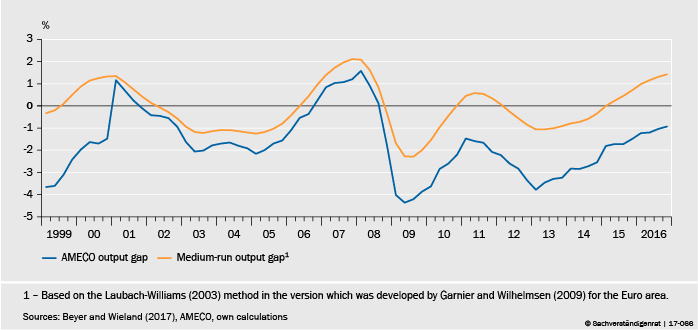
Figure 2 Output gap estimates for the Eurozone
Figure 2 compares the Eurozone output gap estimated along with the medium-run equilibrium interest rate (orange line) to the output gap estimated by the European Commission (blue line). The European Commission estimates an output gap of -1% for 2016. By contrast, the gap calculated with the Laubach–Williams/Garnier–Wilhelmsen methodology is already back in positive territory. This is not surprising. The decline in the estimated equilibrium interest rate is partly due to a decline in estimated potential growth. As a result, estimated potential GDP increases more slowly and actual GDP exceeds the estimated potential by the end of 2014.
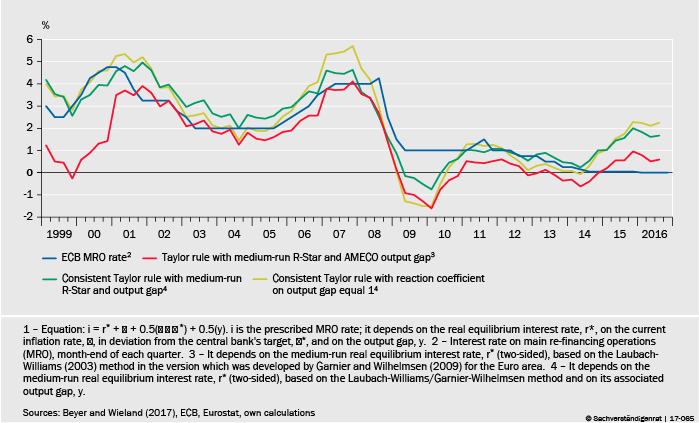
To consider the case for adjusting the policy stance to R-Star, we apply the Taylor rule to the Eurozone. The results are shown in Figure 3. The inflation measure used is the GDP-deflator. The results would be quite similar if core HICP inflation is used instead. The blue line is the ECB rate on its Main Refinancing Operations (MRO) rate.
Figure 3 ECB MRO rate and Taylor rules with medium-run R-Star and output gap estimates
The red line refers to the Taylor rule based on the estimated medium-run equilibrium rate for the Eurozone. Its recommendation for the ECB’s MRO rate currently stands at 0.6%. However, if one uses an estimate of the output gap that is consistent with the estimate of the equilibrium interest rate, the recommended interest rate moves up as shown by the dark-green line (labeled consistent Taylor rule).
Hence, consistent use of the medium-run equilibrium rate and output gap estimates implies that the Taylor rule prescriptions start moving higher than the MRO rate at the end of 2014. This movement is even more pronounced for a version of the rule that assigns a weight of unity to the output gap (light-green line).
ECB policy, however, has been moving in the opposite direction. Overnight money market rates are determined by the ECB’s rate on bank deposits at the central bank which stands at -40 basis points. Additionally, short-, medium-, and long-term rates have been heavily influenced by the large-scale government debt and corporate debt purchase programmes the ECB initiated at the start of 2015. For example, even 10-year yields on German government debt have temporarily been in negative territory. Thus, ECB policy has become much more expansionary relative to the prescriptions of a version of the Taylor rule that responds to Eurozone inflation, output gap, and a reduction in the medium-run R-Star.
These findings indicate that macroeconomic conditions in the Eurozone have improved more than sufficiently for ending the large-scale purchase programmes.
References
Beyer, R C M, and V Wieland (2017), “Instability, imprecision and inconsistent use of equilibrium real interest rate estimates”, CEPR Discussion Paper no. 11927.
Blentzinger, T, and V Wieland (2016), “Forward guidance and ‘lower for longer’: The case of the ECB”, CEPR Discussion Paper no. 11117, London.
Constâncio, V (2016), “The challenge of low real interest rates for monetary policy”, Speech at Macroeconomics Symposium, Utrecht School of Economics, Utrecht, 15 June.
Cukierman, A (2016), “Reflections on the natural rate of interest, its measurement, monetary policy and the zero bound”, CEPR Discussion Paper no. 11467.
Draghi, M (2016), “The international dimension of monetary policy”, Speech, ECB Forum on Central Banking, Sintra, 28 June.
Draghi, M (2013a), “Introductory statement to the press conference”, Speech, press conference of the European Central Bank, Frankfurt am Main, 4 July.
Draghi, M (2013b), “Introductory statement to the press conference”, Speech, press conference of the European Central Bank, Frankfurt am Main, 1 August.
Garnier, J, and B-R Wilhelmsen (2009), “The natural rate of interest and the output gap in the euro area: A joint estimation”, Empirical Economics 36, 297-319.
Holston, K, T Laubach, and J C Williams (2017), “Measuring the natural rate of interest: International trends and determinants”, Journal of International Economics.
Laubach, T, and J C Williams (2003), “Measuring the natural rate of interest”, Review of Economics and Statistics 85, 1063-1070.
Michaelis, H, and V Wieland (2017), “R-Star and the Yellen rules”, VoxEU.org, 3 February.
Taylor, J B, and V Wieland (2016), “Finding the equilibrium real interest rate in a fog of policy deviations”, Business Economics 51 (3), 147-154. See also CEPR Discussion Paper no. 11264.
Taylor, J B (2007), “The Explanatory Power of Monetary Policy Rules”, Business Economics, 42 (4), 8-15.
Taylor, J B (1993), “Discretion versus policy rules in practice”, Carnegie-Rochester Conference Series on Public Policy 39, 195-214.
Yellen, J (2017), “The Economic Outlook and the Conduct of Monetary Policy”, Remarks at Stanford Institute for Economic Policy Research, Stanford University, 19 January.